В начале шестидесятых годов оживился также интерес к акустическим проблемам, главным образом под влиянием исследования Гельмгольца, составившего в данном вопросе эпоху: «Die Lehre von den Tonempfindungen» («Учение о звуковых ощущениях»), которое в промежутке времени от 1863 до 1877 г. вышло в четырех изданиях. Хотя эта работа, как показывает и самое ее заглавие, была предпринята скорее с физиологическими и музыкальными, чем с физическими, целями, но своим ясным и глубоким отношением к трактуемым вопросам она обогатила всю область акустики и, в конце концов, благотворно повлияла даже на чисто механическую часть этой дисциплины.
Гельмгольц делит все звуковые ощущения на шумы и тоны. Вторые вызываются быстрыми периодическими движениями звучащих тел, передаваемыми нашему органу слуха волнообразными движениями воздуха, шумы же возникают вследствие непериодических движений. Тон характеризуется тремя моментами: силой, высотой и тембром. Так как сила звука определяется величиной размаха колебаний, а высота тона — продолжительностью каждого колебания, то относительно тембра остается лишь предположить, что он зависит от формы колебаний. Различные формы колебаний (при равном размахе и продолжительности их) могут различаться друг от друга лишь видом движения в течение периода, различным характером нарастания и убывания скоростей в течение одного колебания. Наиболее простой формой колебаний является такая, при которой скорости колеблющихся частичек изменяются совершенно так же, как при качаниях маятника; поэтому их называют «маятникоподобными» колебаниями, или же, — так как смещение у колеблющейся точки от положения равновесия в любой момент времени выражается формулой
также синусоидальными колебаниями. Все другие виды колебаний, при которых скорости возрастают до максимума иначе, чем в маятнике, или же при которых в течение периода наряду с абсолютным максимумом существует еще один или несколько относительных максимумов скоростей, можно представить себе происшедшими таким образом, как если бы частицам были сообщены простые колебания с числами колебаний, превышающими число колебаний результирующего сложного колебания в один, два, три и т. д. раз. Это было доказано Фурье в его работе «Théorie analytique de la chaleur» («Аналитическая теория теплоты»), где он показал, что всякое регулярное периодическое движение точки может быть представлено при помощи уравнения:
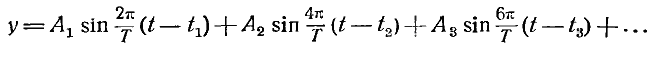
Там же им было доказано, что для каждого заданного периодического движения возможно только единственное подобное разложение на составные простые колебания и что, следовательно, при заданном сложном движении и составные его части задаются однозначно. То, что у Фурье имело чисто механический смысл, у Ома получило акустическую интерпретацию. Согласно последней ухо воспринимает в качестве простого тона только тот звук, который вызван простым синусоидальным колебанием; все же прочие звуки разлагаются на тоны, которые соответствуют отдельным членам ряда Фурье и которые могут быть различаемым в каждом отдельном случае и на слух как основные тоны и добавочные тоны (обертоны). В свое время Август Зеебек решительно оспаривал правильность этого объяснения, утверждая, что всем частным колебаниям, определяемым при помощи ряда Фурье, хотя бы они и имели свои собственные различные по величине периоды, все-таки присущ и общий период колебаний Т; поэтому он утверждал, что ухо в действительности воспринимает только основной тон, соответствующий периоду Т. При этом он отметил, что, например, на сирене он никогда не слышал омовских обертонов или же слышал их настолько слабо, что это никак не согласуется с теорией. Он только допускал, что число членов и величины постоянных в ряде Фурье определяют, быть может, характер звука и, прежде всего его тембр. Теперь Гельмгольц доказал, что мысль Ома о сложном составе звуков была безусловно правильна и что последнее предположение Зеебека с ней вполне совместимо. А именно, во всяком звуке, наряду с основным тоном, существуют и отдельные обертоны, соответствующие ряду Фурье, которых, правда, без особого навыка и внимания наше ухо отдельно не различает, но которые придают основному тону особый тембр. Поэтому он постарался прежде всего доказать, что содержащимся в сложном звуке простым тонам соответствуют особые механические действия во внешнем мире, на основании которых можно установить их объективную природу, независимо от человеческого уха и его ощущений и независимо от теоретических соображений о разложении сложных колебаний на простые синусоидальные колебания. Для этой цели он воспользовался преимущественно явлениями резонанса; он показал, что натянутая перепонка может резонировать не только на звук, равный по высоте ее собственному тону, но и на звуки, в которых собственный тон мембраны содержится как обертон. Подобные же, хотя и более сложные отношения были им установлены и для струн и вообще для всех упругих тел. В качестве наиболее чувствительных приборов для исследования звуков на содержащиеся в них обертоны он предложил применять устроенные им резонаторы, т. е. стеклянные или металлические полые шары или трубки, изображенные на приложенных черт. 15 и 16.
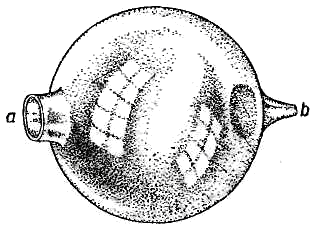

Если подобный резонатор вставить узким концом возможно плотно в ухо, то большинство тонов, раздающихся кругом, бывает слышно значительно более тихо, чем обычно, но зато обертон звука, соответствующий по своей высоте собственному тону резонатора, бывает слышен чрезвычайно громко. Эти приборы Гельмгольца дают возможность производить анализ сложного звука и лицам, не обладающим соответствующим навыком и лишенным музыкального слуха; благодаря этому теория тембра стала доступной для всякого. Поэтому Гельмгольц считает доказанным, что при помощи чисто механического средства, вроде резонирующего тела, из сложной звуковой массы может быть выделен любой входящий в ее состав простой тон и что в звуке музыкального инструмента может содержаться любой простой тон совершенно в таком же смысле, в каком в составе белого цвета солнца или раскаленного тела содержатся различные цвета радуги. Исследовав затем в следующей главе вопрос о том, в какой мере каше ухо способно без помощи искусственных вспомогательных средств различать обертоны и воспринимать их отдельно от основного тона, он приходит к следующим выводам: 1) «Обертоны, соответствующие простым колебаниям в сложном движении воздуха, воспринимаются нами (перципируются), хотя и не всегда доходят до сознания (апперципируются); 2) они могут быть доведены до сознания, или апперципированы, и без всякого искусственного средства, одним лишь надлежащим направлением внимания; 3) однако, и в том случае, когда обертоны отдельно не воспринимаются, а растворяются во всей звуковой массе, их существование в нашем ощущении выражается в изменении тембра звука, причем большая высота их тонов характерным образом выражается в том, что самый тембр кажется ярче и выше по тону». Вместе с тем, однако, Гельмгольц считает необходимым несколько сузить понятие тембра по сравнению с распространенным неясным представлением о нем. Он определенно исключает из этого понятия многое такое, что до сих пор всегда ставилось с ним в связь, а именно, все те особенности звука, которые он приобретает при более или менее постепенном появлении или затухании тона, равно как все те сопутствующие шумы, которые подобно звукам согласных характеризуют тоны духовых инструментов и т. п. Таким образом, под музыкальным тембром он подразумевает только те особенности звука, которые соответствуют длительным равномерным и правильным периодическим движениям воздуха и которые, следовательно, могут быть объяснены только наличием обертонов.
После этого он переходит к детальному исследованию зависимости различных тембров от отдельных сопровождающих их обертонов, и результаты этих исследований формулирует в следующих положениях: «1) Простые тоны, каковы, например, звуки камертонов с резонирующими трубками и звуки широких закрытых органных труб, звучат очень мягко и приятно, без всяких хрипов, но слабо, а в низких тонах глухо; 2) сложные тоны, в которых основной тон сопровождается умеренной силы низшими обертонами приблизительно до шестого,— звучат полнее и музыкальнее предыдущих. По сравнению с простыми тонами они богаче и красивее, но они остаются мягкими и благозвучными до тех пор, пока в них отсутствуют очень высокие обертоны. Сюда относятся звуки фортепиано, открытых органных труб, более мягкие piano человеческого голоса и роговых инструментов. Последние уже представляют собой переход к звукам с высокими обертонами, тогда как флейты и слабые звуки флейтового регистра в органе приближаются к простым тонам; 3) при наличии одних только нечетных обертонов, как это бывает в узких закрытых органных трубках, в струнах фортепиано, ударяемых посредине, и в кларнете, звук становится глухим, а при большем числе таких обертонов — гнусливым. Когда основной тон преобладает по своей силе над обертонами, звук бывает полным, в противном случае он — пустой. Так, звук широких закрытых органных трубок полнее, чем звук узких; звук струн бывает полнее при ударе фортепианным молоточком, чем при ударе палочкой или при щипке пальцем; тон язычковых инструментов при надлежащей надставке бывает полнее, чем без нее; 4) когда очень ясно слышны высокие обертоны дальше шестого или седьмого, то звук становится резким и шероховатым. Причина этого будет показана ниже при рассмотрении диссонансов, возникающих между высокими обертонами. Степень резкости звука может быть различной: при меньшей силе звука высокие обертоны не влияют существенно на музыкальность звука; они даже, наоборот, выгодны для характерности и выразительности музыки. Из этого вида звуков особенно важны звуки смычковых инструментов, большинство язычковых трубок, гобоя, фагота, фисгармонии и человеческого голоса. Более шероховатые резкие звуки медных инструментов производят впечатление большей силы по сравнению с подобными же, но мягкими по тембру звуками. Поэтому сами по себе они мало пригодны для воспроизведения художественной музыки, но производят очень сильное действие в оркестре. Каким образом высокие диссонирующие между собой обертоны придают звуку более пронзительный характер, об этом будет изложено ниже». Но бесспорно наибольшее внимание обратил на себя в исследовании Гельмгольца блестящий успех произведенного им синтеза гласных звуков 2. При помощи чрезвычайно остроумных приборов Гельмгольц поддерживал в состоянии длительного колебания 3 ряд настроенных камертонов, а при помощи резонаторов он по желанию усиливал или ослаблял издаваемые ими тоны. Сначала он для своих опытов применял в качестве основного тона камертон с высотою тона В, а в качестве обертонов семь других камертонов с тонами b, f'', b', d", f", as" и b" Когда резонатор открывали перед камертоном В, слышалось глухое U; если одновременно с ним звучали b и f", звук напоминал U, напеваемое басом. Гласная О получалась при слабом звучании В, сильном звучании b и одновременном слабом звучании b', f' и d". А или, правильнее, Å получалось при наиболее сильном звучании высших обертонов от пятого до восьмого. Для воспроизведения более высоких гласных Гельмгольцу пришлось прибавить еще четыре камертона с тонами d''', f'", as'" и b'". Взяв тогда b в качестве основного тона, он получил гласную А при умеренно-сильном одновременном звучании b' и f" и сильном звучании b" и d'". Для того чтобы звук А перевести в немецкое Ае, следует b' и f" несколько усилить, b" ослабить, a d'" и b'" взять возможно сильнее. Для Е следует первые два наиболее низкие тона, b и b' взять умеренной силы, а высшие f''', as" и b'" взять возможно сильно. Что касается гласной I, то она и с этим набором камертонов еще не могла быть получена. („Подобно гласным человеческого голоса, — говорит Гельмгольц, — могут быть воспроизведены и органные тоны различных регистров, если только в них нет слишком высоких побочных тонов; однако в воспроизведенном звуке нет тех шумов, которые дает воздух, рассекаемый губою трубки. Камертоны воспроизводят только музыкальную часть тембра. Для воспроизведения звуков язычковых инструментов недостает резких высоких обертонов; но гнусливый звук кларнета можно воспроизвести с помощью ряда нечетных обертонов; мягкие же звуки рога получаются при одновременном звучании всего хора камертонов".)
Помимо этого прекрасно удавшегося синтеза, анализ произносимых человеком гласных дал в свою очередь поразительный результат. А именно, Гельмгольц установил, что произносимые ртом гласные звуки образуются не обертонами, находящимися в постоянном отношении к основному тону, а обертонами, абсолютная высота которых не зависит от основного тона. Так, для гласной U характерен составной тон f; для О — составной тон b'; для А — b2; для Е— тоны b3 и f'; для I — тоны d4 и f. Гельмгольц объясняет это тем, что указанные обертоны не являются собственно обертонами звуков, образующихся в гортани, а представляют собой резонансные тоны полостей горла и рта, которые в произнесенном или пропетом звуке усиливают соответствующие им обертоны. А так как эти резонансные тоны полости рта в зависимости от высоты произносимой гласной могут приходиться как на первые, так и на последние ее обертоны, то становится понятным, почему определенные гласные на известные ноты произносятся легче, чем на другие. Хотя в общем, все согласны с приведенными объяснениями Гельмгольца, однако по вопросу об анализе гласных звуков другие исследователи пришли частично к иным, а порою и принципиально отличным результатам; однако ввиду существующего различия в произношении, а также ввиду влияния других побочных обстоятельств это представляется вполне естественным, равно как затруднительным является разрешение вопроса о том, на чьей стороне в данном случае истина. Уже сам Гельмгольц отметил, что измерения характерных для гласных тонов, произведенные до него, не вполне совпадают с результатами его исследований. После Гельмгольца Рудольф Кениг исследовал гласные аналогичным способом и тоже пришел к другим результатам, а именно, для пяти гласных U, О, А, Е и I он нашел в качестве характерных обертонов пять октав, b, b', b2, b3 и b4. В правильности этого ряда Кениг усматривает доказательство в пользу своего мнения, а в простоте этого отношения он видит физиологическую причину того, что во всех языках мы встречаем всегда примерно те же пять гласных, хотя человеческий голос способен создать бесконечное количество различных гласных. На основании многочисленных опытов фон-Цан пришел к выводу, что всякий вообще гласный звук характеризуется не одной или двумя постоянными нотами, а гармоническим рядом более или менее далеко друг от друга отстоящих тонов. Наконец, Э. ван-Квантен оспаривает постоянство характерных тонов в гласных звуках, утверждая, что более низкому основному тону соответствуют и более низкие характерные обертоны, более высокому — более высокие. Феликс Ауэрбах попытался занять в этом отношении среднюю позицию, утверждая, что в каждом гласном звуке содержатся два элемента — абсолютный и относительный, а новейшие работы Германа Грассмана, равно как Флеминга Дженкина и Эвинга, указывают на возможность примирения указанных противоположных взглядов на этой основе. Во всяком случае гельмгольцевское объяснение тембра гласных усилением определенных обертонов благодаря резонансу полости рта остается неоспоримым.
Идя дальше в развитии своей темы о тембре тонов, Гельмгольц затем находит, что различия музыкальных тембров зависят только от присутствия и силы составных тонов, но не зависят от разности их фаз; способность же уха разлагать сложные звуки на составные тоны он объясняет анатомическими его особенностями и, прежде всего устройством так называемого кортиева органа. Этим заканчивается глава о природе отдельных звуков, и затем Гельмгольц переходит к исследованию одновременного действия нескольких звуков. При одновременном звучании двух тонов различной высоты получаются эффекты двоякого рода, а именно — биения, или толчки, и комбинационные тоны. Раньше считали, что между этими двумя явлениями существует лишь степенное различие, так что биения, при достаточной частоте, должны ощущаться как комбинационные тоны. Но Гельмгольц показал, что между этими явлениями существует основное различие. Биения представляют собой чисто интерференционное явление. Когда две волны с одинаковым периодом колебаний встречаются в различных фазах, то, в зависимости от различия фаз, они взаимно усиливают или ослабляют друг друга. Такое изменение сохраняется в постоянном виде, и воспринимаемый нами тон остается неизменным. Если же встречаются волны с различными периодами, то они, в зависимости от отношения числа колебаний, периодически то усиливают, то ослабляют друг друга, и наше ухо воспринимает эти усиления и ослабления как толчки или биения. Для этих биений имеет силу закон, установленный уже Гэллстремом. Число биений в определенный промежуток времени равно разности чисел колебаний обоих тонов за то же время. Хотя комбинационные тоны, известные уже с давнего времени, и следуют тому же закону, тем не менее происхождение их все-таки нельзя сводить к биениям.
Помимо этого вида комбинационных тонов, которые Гельмгольц, согласно закону Гэллстрема, назвал разностными тонами, он нашел еще новый вид комбинационных тонов, названный им суммовым тоном, так как число их колебаний равно сумме чисел колебаний тонов, которые их вызывают. Вообще же причины возникновения комбинационных тонов сводятся, по его мнению, к следующему: «До сих пор всегда принимали, что различные звуковые волны, возбужденные в воздухе или в другой упругой среде, просто складываются, не оказывая друг на друга никакого влияния; это допущение считали в достаточной мере доказанным тем фактом, что при одновременном звучании музыкальных инструментов или человеческих голосов мы в состоянии различать в отдельности каждый инструмент или голос со свойственными им высотою и тембром. Но, с другой стороны, следует принять во внимание, что возможность такого простого сложения волн теоретическая механика доказала лишь для бесконечно малых колебаний; между тем из уравнений движения воздуха можно усмотреть, что при колебаниях с конечной величиной амплитуд такое простое сложение не может иметь места.
Теоретическое исследование случаев последнего рода мне показало, что различные простые колебания упругого тела накладываются беспрепятственно друг на друга до тех пор, пока амплитуды колебаний настолько малы, что вызванные смещениями движущие силы примерно пропорциональны самим смещениям. Но когда амплитуды колебаний возрастают настолько, что квадраты смещений уже заметно влияют на величину движущих сил, то возникают новые системы простых колебательных движений, периоды которых соответствуют периодам известных комбинационных тонов». Комбинационные тоны слышны лишь тогда, когда два музыкальных тона различной высоты звучат одновременно сильно и равномерно. Но в этом именно случае результирующее движение нельзя, как при интерференции, рассматривать как простую алгебраическую сумму составных движений, — при рассмотрении его следует непосредственно обращаться к действующим силам. Силу, которая при подобных условиях после смещения массы m в упругой среде на расстояние х стремится вернуть ее в положение равновесия, Гельмгольц принимает равной ах+bх2. Если при этом на одну и ту же точку действуют две системы волн с силами fsin(pt) и gsin(qt+c), то уравнение ее движения приобретает следующий вид:
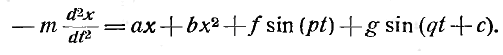
Это уравнение можно проинтегрировать с помощью ряда, если положить
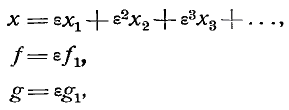
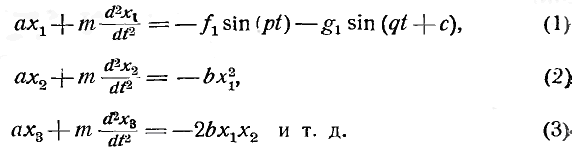
Из уравнения (1) получается путем интегрирования, если положить:
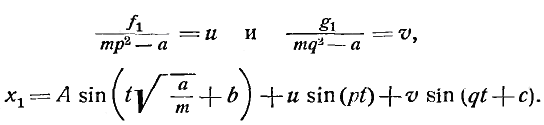
Это — знакомый результат для бесконечно малых колебаний; в нем выражены три тона: собственный тон точки m и оба сообщенных ей тона с числами колебаний р и q. Так как собственный тон быстро затухает, то А можно положить равным нулю; тогда путем подстановки x1 в уравнении (2) получаем:
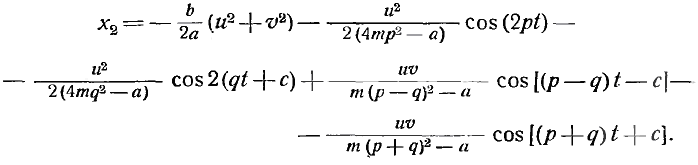
Таким образом, второй член ряда для х содержит, кроме одной постоянной величины, тоны с числами колебаний 2р, 2q, (р—q) и (p+q), т. е. первые обертоны р и q, а также первый разностный и первый суммовой тоны тех же тонов. Амплитуды этих комбинационных тонов пропорциональны произведению uv, и, следовательно, при малых амплитудах первичных тонов они представляют собою малые величины второго порядка и возрастают с амплитудами первичных тонов в отношении квадратов. Отсюда понятно, почему при слабых первичных тонах комбинационные тоны не слышны и почему суммовой тон всегда слабее разностного. Путем разложения высших членов х3, х4 и т. д. можно дальше аналогичным образом получить высшие обертоны, а также комбинационные тоны высших порядков.
Построив, таким образом, теорию комбинационных тонов на новых основаниях и совершенно отделив их от биений, Гельмгольц в соответствии с этим показал, что последние ощущаются нами как толчки, даже и в том случае, когда их частота далеко перешагнула через нижнюю границу нашего звукового восприятия. Правда, когда их частота становится больше чем 39 в секунду, толчки уже не воспринимаются каждый в отдельности, но их действие проявляется в том, что звук становится неровным, дребезжащим, шероховатым. Интересно, что граница восприятия биений зависит не только от их числа, но также и от соответствующих интервалов тона. Так, например, полутон в верхней октаве дает еще ясные биения, тогда как малая терция в нижней октаве их не дает, несмотря на то, что в первом случае биения следуют друг за другом гораздо чаще, чем во втором. Гельмгольц объясняет это явление тем обстоятельством, что биения бывают слышны лишь в том случае, когда возбужденные концы нервов в кортиевом органе лежат близко друг от друга, т. е. когда соответствующий интервал тонов не превышает известного предела.
Быстрые биения дают возможность еще глубже проникнуть в особенности наших звуковых ощущений. Всякое прерывистое раздражение наших нервных аппаратов возбуждает их сильнее, чем длительное равномерное раздражение. Подобно тому как мерцающее пламя утомляет и раздражает глаз, так и интервалы, вызываемые быстрыми биениями, неприятны для уха. Поэтому подобные интервалы, образующие спутанную массу тонов, трудно разложимую на элементы, ощущаются нами как диссонансы, тогда как интервалы, тоны которых следуют друг за другом равно, без биений, дают ощущение созвучия. Ввиду специально физического характера настоящего сочинения и за недостатком места мы не можем здесь входить в описание того, каким образом Гельмгольц дальше на основании биений между первичными тонами, между обертонами и комбинационными тонами устанавливает условия созвучия и аккорда и затем на этой базе строит основные законы гармонии. Однако уже из приведенного можно видеть, какое большое значение имеет работа Гельмгольца и для физики в тесном смысле. Гельмгольц блестяще показал на примере и, пожалуй, более ясно и сознательно, чем когда-либо раньше до него, каким образом физика может свести особенности наших ощущений, их различия по силе и по качеству, к движениям или к изменениям движений и, таким образом, сделать величины ощущений доступными даже для математической обработки.
В этом отношении сочинение Гельмгольца, которое, вообще говоря, как будто стоит в стороне от общего русла новейшей физики, вплотную приближается к осуществлению ее цели, заключающейся в том, чтобы свести все явления природы к движениям. Что касается того обстоятельства, что в конце своего труда Гельмгольц ставит себе как натуралисту известную границу и исключает из своей задачи все, что относится к музыкальной эстетике, поскольку в этой области действуют психические моменты, — то здесь он дает пример научной сдержанности, который можно смело рекомендовать многим психологам и философам.
Результаты усиленного внимания, оказанного Гельмгольцем сложению музыкальных тонов, а вместе с тем и сложению колебаний и волновых движений, скоро проявились в быстром конструировании и усовершенствовании приборов, предназначенных для разложения сложных звуков, причем, идя навстречу требованиям времени, при этом стремились также и к объективному наглядному изображению этих явлений. Прежде, когда речь шла, главным образом, о том, чтобы облегчить понимание волнообразного движения, строились приборы, показывавшие наглядно процессы колебания и распространения волн, а также их сложение. Так, И. Г. Мюллер в 1846 г. применял стробоскопический диск, или «колесо жизни», для демонстрирования колебательных и волновых движений с помощью специально для этой цели нарисованных шаблонов. Около того же времени Уитстон построил волновую машину, открывшую собою серию приборов, в которых ряд иголок или маятников с блестящими головками принимал форму определенной волны путем перемещения под ними или путем наложения на них моделей волн. Из чисто последних особенно был известен усовершенствованный прибор Фесселя; после этого подобные машины, с различными усовершенствованиями для наглядного изображения или даже для создания новых комбинаций волн, продолжали конструироваться вплоть до новейшего времени. Но наряду с устройством подобных волновых моделей усердно занялись устройством и таких приборов, которые давали бы возможность непосредственно наблюдать отдельные колебания и их составные элементы, достигая при этом возможно большей точности. С целью изучения колебаний струн Томас Юнг обматывал их серебряной нитью и рассматривал в темной комнате, направляя на избранную точку струны сильный пучок света. По существу аналогичный метод применил в 1855 г. Лиссажу для наблюдения сложения колебаний и для сравнения этим путем колебаний исследуемого тела с нормальными колебаниями другого тела. С этой целью он снабжал оба колеблющихся тела, обыкновенно два камертона, колебания которых он хотел сложить или сравнить, двумя маленькими зеркальцами и затем направлял сильный пучок света таким образом, что, упав на одно из зеркалец, он отражался от другого, а затем падал на экран. Обыкновенно Лиссажу устанавливал колеблющиеся тела таким образом, что плоскости их колебаний были перпендикулярны друг к другу; тогда при колебаниях в унисон на экране получался светлый эллипс, а при других соотношениях тонов получались более сложные фигуры, которые получили название фигур Лиссажу. Для более точного, хотя и субъективного наблюдения этих фигур он заменял зеркальце на сравниваемом теле объективом маленькой зрительной трубки; луч, отраженный от первого вибрирующего тела, проходил через этот колеблющийся объектив, а затем через неподвижный окуляр попадал в глаз наблюдателя. Гельмгольц при своих исследованиях применил такой же прибор в несколько измененном виде в качестве вибрационного микроскопа. Лиссажу использовал свой прибор для подробного изучения сложения колебаний и тонов, а главным образом для проведения порученной ему во Франции проверки нормальных камертонов, для которых в 1859 г. там было установлено нормальное а в 870 (половинных) колебаний.
Для наблюдения воздушных колебаний пуховых инструментов и для настройки их, конечно, нельзя непосредственно применить метод Лиссажу; для этой цели следует сообщить эти колебания сначала каким-нибудь твердым телам, лучше всего тонким перепонкам. Подобным приемом впервые воспользовался в 1859 г. Э. Скотт; однако он совершенно отказался от световых фигур Лиссажу и предпочел регистрировать колебания перепонки прямо при помощи присоединенного к ней пишущего штифта. Правда, этот графический метод не был придуман самим Скоттом, его уже раньше неоднократно применяли в различных видах. В 1830 г. В. Вебер наносил колебания камертона на закопченное стекло, слегка проводя по последнему камертоном, к одной из ножек которого было прикреплено упругое острие. Дюгамель установил упругие острия, прикрепленные к колеблющимся струнам и прутьям, таким образом, что они слегка касались закопченной поверхности цилиндра, который приводился во вращение рукояткой около оси с винтовой нарезкой. Количество гребней и впадин звуковых волн, получавшееся при этой записи, давало абсолютное число колебаний за соответствующий промежуток времени. Конечно, и обратно, если наперед известно число колебаний тела в секунду, можно по числу вычерченных на барабане колебаний определить величину соответствующего промежутка времени. Таким образом, графические виброскопы можно было применить в качестве хроноскопов и это именно обстоятельство сильно содействовало их усовершенствованию. Вертгейм применил при своих исследованиях метод Дюгамеля но, найдя, что вращение цилиндра недостаточно равномерно, а следовательно, и измерение времени недостаточно точно, он присоединил к прибору нормальный пишущий камертон, дававший 256 колебаний в секунду. При помощи этого усовершенствованного прибора он, по его словам, получил возможность измерять время с точностью до 1/2560 сек.
Однако мысль о превращении виброскопов в приборы для измерения времени стала планомерно проводиться лишь позднее, и идея хроноскопии получила толчок совсем с другой стороны. Пуллье в 1844 г. попытался наладить измерение очень малых промежутков времени следующим образом: он допустил, что при очень кратковременном замыкании тока отклонение стрелки гальванометра пропорционально продолжительности тока, и по показаниям гальванометра судил о длительности тока. В том же году Брегэ описал другую форму хроноскопа, который он разработал совместно с русским артиллерийским офицером Константиновым. На цилиндр, равномерно вращающийся около горизонтальной оси, в начале и конце движения опускались при помощи электрического тока металлические штифты, которые и отмечали соответствующие моменты времени. Статья Брегэ вызвала возражение со стороны Уитстона, который, заявляя о своем первенстве в этом изобретении, указал, что такого типа приборы он послал в 1840 г. Брюссельской академии наук, а в 1842 и 1843 гг. — Константинову. Различие между этими приборами заключалось, по его словам, лишь в следующем: Уитстон заметил, что штифты падают на цилиндр не в надлежащие моменты, поэтому он оставил свою первоначальную идею и устроил прибор таким образом, что штифт писал на цилиндре, вращающемся около оси с винтовой нарезкой, сплошную спиральную линию, которая в нужные моменты прерывалась. Bepнep Сименс вместо штифта воспользовался для отметок электрическими искрами, которые перескакивали на цилиндр и не влияли на равномерность его хода. Но так как в дальнейшем выяснилось, что и часовой механизм, которым был снабжен цилиндр, не обеспечивает достаточно равномерного хода аппарата в течение продолжительного времени, то Гипп в 1848 г. усовершенствовал уитстоновский хроноскоп, устроив таким образом, что часовой механизм каждую секунду спускал на цилиндр второй штифт, который делал там отметку; таким образом, нормальный промежуток времени, с которым надлежало сравнивать измеряемые отрезки времени, был ограничен одной секундой. После этого перешли к тому, что на цилиндре наряду с началом и концом изучаемого явления стали регистрировать еще значительно меньшие промежутки времени; для этой цели на цилиндре стали наноситься одновременно колебания нормального камертона. На этом именно принципе устроили свои хроноскопы Лаборд, В. Беетц, И. Г. Мюллер и особенно удачно Р. Кениг. На первых порах измерительный камертон приводился в движение просто смычком, но затем Беетц стал для этой цели применять электромагнитную установку Гельмгольца, при которой он мог получать колебания любой продолжительности. С этой же целью Кениг в приборах более простого устройства применял кроме пишущего камертона еще второй камертон с равным числом колебаний; последний он приводил в движение с помощью смычка, а благодаря резонансу приходил в колебание и пишущий камертон; эта установка давала более равномерные колебания пишущего камертона. Начало и конец определенного промежутка времени по-прежнему отмечались при помощи искры или при помощи автоматически падающих штифтов с остриями.
И упомянутый выше пластинчатый фонограф Скотта, или фонавтограф, как его называл сам Скотт, тоже получил в это время большое значение, правда, не столько сам по себе, сколько благодаря приборам, которые были построены на том же принципе. Фонавтограф состоял из полого гипсового сосуда эллипсоидальной формы, в одном фокусе которого помещалось звучащее тело, а в другом находилась мембрана, воспринимающая звуковые колебания. Прикрепленный к наружной поверхности последнего небольшой штифт записывал колебания перепонки на вращающемся цилиндре. Кениг усовершенствовал этот прибор только в том отношении, что он придал воспринимающему сосуду параболическую форму, а в качестве материала для сосуда взял цинк; новый очень интересный метод наблюдения воздушных колебаний с помощью мембран он применил при устройстве своих известных манометрических пламен. Манометрическое пламя получалось при горении газа, вытекающего из сосуда, одна стенка которого состояла из упругой перепонки; когда на эту перепонку падали звуковые колебания, это вызывало соответствующие колебания пламени. Кениг сначала ставил манометрическое пламя в узлах звучащих органных трубок для того, чтобы сделать видимыми происходящие там попеременно сгущения и разрежения воздуха; но затем он соединил его с воспринимающей частью фонавтографа для того, чтобы с помощью манометрического пламени изучить различные звуковые колебания 7.
Вращающиеся зеркала, примененные Кенигом для наблюдения колебаний пламени, принадлежит по своей идее Уитстону 8, который уже в 1834 г. при своих работах по измерению скорости электричества производил при помощи таких зеркал анализ движения пламени; позднее с этой же целью Тиндаль применил трехгранную призму с зеркальными сторонами, которая, будучи подвешена на нити, вращалась вследствие раскручивания этой нити. Манометрическое пламя Кенига представлялось сначала по сравнению с фонавтографом скорее интересной физической игрушкой, чем научным измерительным прибором, однако очень скоро оно стало применяться с большим успехом для изучения гласных звуков, хотя этот метод и оказался не вполне надежным, фон-Цан при своих упомянутых выше исследованиях нашел, что для анализа высших гласных звуков изображения этих пламен могут дать лишь немногое, и высказал мысль, что этот пробел может быть восполнен фотографированием этих изображений, благодаря чему и представится возможность спокойно производить количественные измерения. Ауэрбах при изучении гласных, помимо манометрического пламени применил еще два других способа и получил, таким образом, возможность выяснить их сравнительные достоинства. Сначала он считал способ Кенига, ввиду объективности и четкости даваемых им изображений, наилучшим, но затем убедился, что изменчивость давления газа, вращение зеркала и в особенности свойства перепонки, передающей колебания, заметно влияют на форму пламени. После этого он стал применять для этой цели резонаторы, покрывая отверстие их узкого конца, вставляемого обычно в ухо, мыльной пластинкой и наблюдая колебания последней по старому методу Лиссажу с помощью световых зайчиков. И все-таки, в конце концов, обычный субъективный анализ звуков на слух при помощи резонаторов пришлось признать наиболее надежным. Однако позднее Г. Грассман указал, что и резонаторы изменяют первоначальное соотношение сил отдельных тонов, и признал недостаточным все вообще искусственные средства для анализа гласных звуков.
В еще более непосредственной связи с фонавтографом, чем регистрация пламенем, находятся фонограф Эдисона и телефон — аппараты, которые, конечно, могли бы быть и прямо сконструированы, исходя из устройства нашего слухового органа, и, вероятно, в конечном счете, построены та этом принципе. О телефоне у нас будет речь ниже; об эдисоновском же фонографе мы здесь заметим только, что он впервые был описан 22 декабря 1871 г. в «Scientific American», XXXVII, стр. 384 и 11 марта 1878 г. был продемонстрирован (впервые на нашем континенте) перед Парижской академией наук. Хотя по существу он представляет собою не что иное, как фонавтограф Скотта, приспособленный для использования его в обратном направлении, однако для осуществления этого аппарата потребовались, период времени в 20 лет и работа первоклассного изобретательского гения.
Аппараты, в которых колебания воздуха передаются перепонкам и, обратно, распространяются последними, до известной степени разрешили старый спор о колебаниях упругих пластинок. Савар утверждал, что перепонка способна воспринимать любые тоны, высота которых выше собственного ее тона, и с этой точки зрения объяснял функции нашей барабанной перепонки в процессе восприятия звука. Однако Пуассон и Ламе теоретически, а Ж. Бургэ и Ф. Бернар также и экспериментальным путем пришли к иным выводам. В 1862 г. Радо снова высказался в пользу прежнего мнения, согласно которому упругие пластинки могут воспроизводить лишь отдельные свойственные им, в соответствии с их величиной, массой и т. п., основные тоны и обертоны.
Однако приведенные выше аппараты вполне определенно показали, что при известных условиях перепонки способны воспроизводить любые тоны, хотя они и изменяют тембры и свойства тонов. В соответствии с этим взглядом Эльзас прямо показал, что всякое упругое тело при надлежащем воздействии может давать любой вид колебаний, но только, в зависимости от расстояния между вынужденным тоном и тоном собственного колебания тела, воздействие на тело должно быть более или менее сильным и интенсивность самого вынужденного колебания бывает больше или меньше.
Газовое пламя оказалось чувствительным к воздушным колебаниям еще и в другом, более свободном виде, чем в виде манометрического пламени Кенига. Шаффготш в 1857 г. открыл в загадочной химической гармонике новые удивительные свойства и этим значительно оживил интерес к данному явлению. А именно, он заметил, что если поблизости от пламени химической гармоники возбуждается музыкальный тон, который звучит (приблизительно) в унисон с тоном гармоники или на октаву выше, то пламя приходит в возбуждение, сильно колеблется вверх и вниз, а при достаточной силе внешнего звука даже гаснет. При высоких собственных тонах гармоники сильные фальцетные ноты человеческого голоса заставляли ее умолкнуть на расстоянии в 10—12 шагов; того же можно было достичь хлопаньем в ладоши и другими шумами; а сильный органный тон действовал на пламя, усиливая или туша его, даже на расстоянии в 44 м. После этого Тиндаль на опытах с сиреной установил зависимость данного явления от высоты внешнего тона и собственного тона пламени. Когда тон сирены постепенно приближался к тону пламени, начиная с более низких нот, то пламя колебалось все медленнее и медленнее и, наконец, колебания его прекращались, когда оба тона сравнивались; при дальнейшем повышении внешнего тона колебания снова постепенно учащались и, наконец, становились незаметными. Таким образом, пламя своими движениями оптически воспроизводило акустические биения обоих тонов. При известной высоте трубки пламя звучало всего легче; ниже и выше этого места его можно было по желанию заставить петь или замолкнуть, причем оно не гасло. Десять лет спустя Тиндаль исследовал новое явление чувствительного пламени, которое подметил его ассистент Баретт и которое находится в несомненной связи с поющим пламенем. А именно, когда зажженный газ находится под столь сильным давлением, что пламя близко к вспышке, то оно приходит в сильное колебание и начинает то укорачиваться, то удлиняться, лишь только поблизости от него раздается тон надлежащей высоты. Эти процессы можно рассматривать как явления резонанса, и, действительно, Планету удалось показать, что эти пламена, подобно резонаторам, способны усиливать звуки камертонов.
Тем не менее, способность пламени приходить в колебание до сих пор еще не объяснена, и общей теории колебания пламени пока еще не существует или, по крайней мере, не существует еще общепризнанной теории. Более старая гипотеза, подкрепленная авторитетом Фарадея, заключающаяся в том, что звучание пламени происходит вследствие прерывистости горения, как будто еще в 1866 г. была подтверждена наблюдениями слоистости поющего пламени. Однако уже в 1858 г. Грайлих и Вейсс объяснили данное явление более естественно не периодическим потуханием пламени, а изменениями объема, происходящими при горении газа, притоком кислорода, удалением продуктов горения и поднятием по трубке нагретого воздуха. В пользу последнего обстоятельства особенно сильно говорили опыты П. Л. Рийке, который вызывал звучание в трубках без всякого пламени, накаливая в них электрическим током металлические сетки. Зондгаус в 1860 г. вывел из своих опытов заключение, что причина данного явления заключается в колебаниях самого воздуха в вытечной трубке; он указал при этом на звуки, возникающие при вытекании воды, и сравнил этот процесс с возникновением тонов в языковых трубках. И. Б. Цох, пытаясь хотя бы частично отстоять гипотезу Фарадея, указал, что верхушка пламени периодически то тухнет, то загорается. А. Терквем объяснил звучание трубки взаимодействием между пламенем и вызываемым им восходящим током воздуха; этот ток изменяет форму пламени, а последнее в свою очередь действует на ток воздуха, так что вся система начинает совершать правильные колебания. Наконец, Брезина объяснил данное явление тем, что входящий в трубку воздух под пламенем замедляется, вследствие чего в этом месте образуется сгущение, которое, выравниваясь в обе стороны, вызывает колебания.
Возможно, что многие или даже все приведенные причины влияют на звучание пламени, однако новейшие работы над родственными явлениями заставляют нас в большей мере, чем раньше, предполагать, что звуки пламени, подобно всем вообще звукам, возникающим при движении воздушных масс, происходят вследствие сопротивления, которое встречает газ, протекая мимо другого газа, или мимо твердых тел, — что они, следовательно, должны быть отнесены к разряду звуков от трения. Другими словами, поступающий в трубку воздушный ток приходит в колебания вследствие трения о края и стенки трубки, равно как о пламя и, в случае соответствия этих колебаний собственному тону трубки, они приобретают характер регулярного звука. Подобного рода объяснения были уже предложены в 60-х годах Тиндалем и Кундтом, а последний 7, в частности, показал, что подобные звуки от трения можно воспроизвести и на свободном пламени. Привлеченный случайным звучанием: широких пламен светильного газа, Кундт путем наблюдения установил, что два встречных тока воздуха, вытекающих из тонких заостренных трубок, дают легкие тоны, когда струи неодинаково интенсивны или же когда они направлены не прямо друг против друга, а несколько в сторону. Направленные таким же образом струи горящего светильного газа издавали более сильные звуки. Однако подобные тоны возникали и в том случае, когда одно из этих пламен заменялось струей атмосферного воздуха или угольной кислоты, и — что представлялось убедительнее всего — они были слышны и тогда, когда пламя направляли и просто на стену.
Многочисленные, вызывавшие большой интерес работы о трении газов и жидкостей друг о друга, а также о твердые тела, естественно повлекли за собою дальнейшие исследования о звуках от трения. Во всех случаях, когда газ или жидкость движется мимо твердых тел или же, наоборот, твердые тела движутся в газах или жидкостях, должны, как при трении друг о друга твердых упругих тел, возникать шумы, и последние могут перейти в тоны, если движения достаточно правильны или если вблизи имеется тело, которое способно выделить эти тоны из шума путем резонанса. Первую большую работу о подобных тонах от трения опубликовал в 1878 г. В. Стругаль. Он укрепил на вертикальной оси друг над другом два передвижных горизонтальных плеча, между которыми можно было натягивать тела, исследуемые с точки зрения звуков от трения (металлические проволоки, стеклянные палочки, стеклянные трубки), и затем при помощи махового колеса приводил рукою ось в быстрое вращение. Эти опыты привели его к следующим законам: высота тона от трения не зависит ни от вещества, ни от степени натяжения, ни от длины проволоки; она прямо пропорциональна скорости ее движения и обратно пропорциональна ее толщине; с увеличением длины проволоки возрастает и сила звука. Если у тонких упругих проволок движение постепенно ускорять, то сила тона несколько раз нарастает до значительных максимумов, причем это случается всякий раз, когда тон от трения совпадает с собственным тоном (основным или обертоном) проволоки. Значит, при достаточной силе воздействия сама проволока приходит в звучание, когда колебания воздуха, вызванные трением, соответствуют ее тону. Однако тот факт, что при увеличении вращательной скорости тон от трения по своей высоте опережает тон продолжающей еще звучать струны, ясно свидетельствует о том, что тоны от трения существуют самостоятельно. Отсюда, конечно, следовало, что звуки эоловой арфы являются тонами от трения, или тонами струн, вызванными трением. Точно так же и звуки губных трубок Стругаль объясняет трением воздушного тока о губу инструмента. К этому мнению присоединился в своей «Акустике» 1883 г. и Мельде, который дальнейшими опытами тоже установил зависимость тонов губных трубок от тонов трения. Изменяя различным образом давление, а, следовательно, и скорость, с которой воздух входит в трубку, он пришел к следующему закону: в органной трубке может зазвучать обертон, когда он становится обертоном по отношению к тону от трения, получаемому от вдувания в трубку воздуха; сила тона данной трубки повышается тем больше, чем больше этот тон является тоном сильнейшего резонанса, т. е., когда последний звучит в унисон с тоном от трения. Тоны поющего волчка Мельде тоже объясняет тонами от трения, возникающими в отверстии волчка и усиливаемыми резонансом его полости.
Но, во всяком случае, в губных инструментах следует различать тоны от трения двоякого происхождения: одни, соответствующие стругалевским тонам, возникающие на губе, и другие, возникающие на краях воздушной щели. Последние внимательно исследовал В. Кольрауш в 1881 г. При этом он пришел к выводам, вполне соответствующим положениям Стругаля, и на этом основании признал доказанным, что тоны от щели, подобно стругалевским тонам, возникают вследствие трения движущихся масс воздуха о соответствующие твердые тела или же о слои воздуха, приставшего к твердым телам. Аналогичным образом Э. Сорель объясняет замеченные путешественниками в пустынных местах звуки наполовину струнного, наполовину колокольного характера. Он полагает, что эти звуки представляют собою тоны от трения воздушных токов о выступы скал или гребни гор, усиливаемые долинами, как резонаторами.
Хотя в физике уже давно проводилась усиленная работа над общими вопросами о превращении сил, тем не менее, акустика вплоть до новейшего времени оставалась в стороне от этого общего движения. Но теперь, когда было выявлено так много разнообразных случаев превращения механических движений в звуковые колебания, обратились, наконец, и к проблеме о превращении звуков в иные формы движения. Э. Варбург пришел к выводу, что при звучании твердых тел некоторая часть звуковой энергии всегда превращается в теплоту и тем большая, чем скорее прекращается звучание. Подобное нагревание установили сначала при продольных колебаниях твердых тел, а затем и при поперечных; однако в хорошо высушенных газах (атмосферном воздухе, угольной кислоте и светильном газе) не было замечено какого-либо образования теплоты. В 1872 г. Шампион и Пелле нашли, что при благоприятных условиях звук может освобождать химические силы; так, например, йодистый азот взрывается при наличии определенных высоких тонов. Артур Христиани в 1882 г. показал, что в некоторых случаях резонаторы способны поглотить тоны, не издавая звуков, а непосредственное превращение звуковых движений в электричество в телефоне Белла представило с этой точки зрения особый интерес.
Отсюда сама собою возникла мысль об измерении звуковой энергии, об отношении между силой звука и теми силами, которые его вызывают; разработка сонометрии стала насущной задачей физики. Однако для оценки сравнительной интенсивности различных тонов звука ухо еще менее пригодно, чем глаз для оценки света; поэтому устройство сонометров не только заставило ждать себя дольше, но и до сих пор оно удалось в значительно меньшей степени, чем устройство фотометров. Правда, физиологи многократно занимались определением чувствительности уха к различиям в интенсивности звука, то при этом измерялась собственно не сила звука, а величина живой силы, примененной для получения звука. Прибор для объективного сравнения сил звуков попытался устроить А. М. Майер. Звуки из двух источников, находившихся в отдельных комнатах, он воспринимал одинаково настроенными резонаторами и затем по трубкам одинаковой длины направлял в манометрическую капсулу кениговского прибора. Спокойное состояние манометрического пламени указывало на равенство сил обоих звуков, воспринимаемых резонаторами, а по расстоянию последних от источников звуков исчислялась, по закону убывания силы звука пропорционально квадратам расстояний, — сила звуковых источников. В. Дворак в 1877 г. указал, что и с помощью изобретенных им приборов для демонстрирования акустических притяжений и отталкиваний можно было бы измерять энергию звуковых движений, а, следовательно, и интенсивность звуков. Наконец, А. Обербек, вспомнив замечание В. Вебера, сделанное им в 1846 г., что силу звуковых движений можно было бы измерять вызываемыми ими при некоторых условиях индукционными токами, воспользовался им следующим образом. Введя в цепь гальванического тока микрофон и гальванометр, он наблюдал колебания стрелки, вызываемые звуками, действовавшими на микрофон, принимая их в известных пределах пропорциональными силам звуков; к сожалению, при этом выяснилось, что микрофон неодинаково чувствителен к различным звукам. Обербек применил свой прибор, главным образом, для выяснения того, какая доля энергии, сообщаемой звучащему телу, действительно превращается в звуковое движение. Для силы звука, вызываемого падением свинцовых или каменных шаров на деревянную доску, он принял эмпирическую формулу J=р•he, где р обозначает вес падающего тела, h — высоту падения, а e — некоторую постоянную величину. Наблюдая затем отношение сил звуков при падении некоторого тела с различных высот, он получил из приведенной формулы для e значения, колебавшиеся между 0,629 и 0,656. Раньше него Фирордт определил для различных шаров высоты падения, при которых по субъективной оценке ухом получались звуки одинаковой силы; из этих опытов для e определилось число 0,622.
Обербек полагает, что возможность применения микрофона в качестве сонометра выяснится только в результате дальнейшей разработки, но указывает, что по своей чувствительности микрофон, во всяком случае, значительно превосходит все аппараты, применявшиеся до сих пор для изучения звука.
Новая кинетическая теория газов вызвала некоторую тревогу в области теории распространения звуков в газах. Едва только в начале шестидесятых годов, наконец, пришли к единогласию по вопросу о поправке Лапласа к формуле Ньютона, как все привычные дедукции снова были поставлены под знак вопроса механической теорией газов. Раньше распространение звука представляли себе, как передачу движения в покоящейся среде; теперь же колебания должны были передаваться от частицы к частице, причем все они сами по себе уже обладали значительными скоростями; поэтому на движения отдельных молекул в газе, проводящем звук, уже нельзя было смотреть исключительно как на звуковые колебания. Но, с другой стороны, нетрудно было сообразить, что в среде, в которой происходят внутренние движения, сгущения и разрежения должны распространяться, как в покоящейся среде. Так, например, если в газе колеблется какая-нибудь плоскость, то при своем движении вперед она будет отражать от себя ударяющиеся об нее молекулы с большею скоростью, чем та, какую они имели в момент удара. Эту увеличенную скорость молекулы при своих столкновениях будут передавать другим молекулам, и эта передача, равно как и уплотнение, вызванное увеличенной скоростью, будет распространяться по всему газу. То же самое будет происходить и с разрежением при попятном движении упомянутой плоскости. Таким образом, все различие в распространении звука по старой и новой теориям будет заключаться лишь в том, что в первой предполагается передача всей скорости, а во второй передача разности скоростей. При этом, однако, остается одно значительное затруднение. Так как передача разностей скоростей происходит благодаря движению газовых частиц, то можно было бы думать, что скорость этой передачи, а значит, и скорость распространения звука должны быть равны скорости движения молекул соответствующего газа, а между тем это, как известно, не соответствует действительности. И. Стефан, первый высказавшийся в литературе о распространении звука с точки зрения новой теории газов, указал на это затруднение уже в 1863 г. По-видимому, — говорит он, — до сих пор никто не обратил внимания на то обстоятельство, что если допустить в газах правильное расположение молекул, как его представлял себе Крениг, то из новой теории газов можно получить для скорости распространения звука ньютоновскую формулу. По этой теории скорость звука должна зависеть от скорости поступательного движения молекул и обе скорости были бы почти равны, если бы скорости всех молекул имели направление, одинаковое с направлением распространения звука. Но если мы представим себе, по Кренигу, пространство разделенным на кубики, в каждом из которых движутся параллельно сторонам кубика только три молекулы, и то же пространство разделенным еще на слои плоскостями, перпендикулярными к диагональным осям кубиков, то движение от слоя к слою будет распространяться лишь со скоростью х=u/![]() 3, где u обозначает поступательную скорость молекул. Если, далее, мы обозначим через m массу одной молекулы, через v — определенный объем, через n — число молекул в этом объеме и через р — существующее давление, то, по Кренигу и Клаузиусу, pv=mnu2/3. Отсюда, если mn/v, т. е. плотность газа, обозначить через r, мы получим формулу Ньютона: х=
3, где u обозначает поступательную скорость молекул. Если, далее, мы обозначим через m массу одной молекулы, через v — определенный объем, через n — число молекул в этом объеме и через р — существующее давление, то, по Кренигу и Клаузиусу, pv=mnu2/3. Отсюда, если mn/v, т. е. плотность газа, обозначить через r, мы получим формулу Ньютона: х=![]() (p/r).
(p/r).
Однако этот вывод скорости распространения звука на основе новой теории газов, остававшийся долгое время без изменения, не мог дольше остаться в силе после того, как Клаузиус, Клерк, Максвелл, О. Е. Мейер и Руше отказались от простоты крениговских допущений и даже допустили неравенство скоростей молекул в одном и том же газе. Поэтому Гоорвег попытался построить вывод скорости распространения звука на самых общих основаниях кинетической теории газов, но, в отличие от Стефана, замедление звука по сравнению со скоростью молекул он объяснил потерей времени, испытываемой молекулами при их столкновениях. Тольвер Престон при разработке того же вопроса вернулся, наоборот, к точке зрения Стефана на причину замедления скорости. Вопрос об отношении скорости звука к скорости молекул получил тем больший интерес, что отношение это для всех газов, или, по крайней мере, для газов одинакового молекулярного строения, должно было оставаться приблизительно постоянным и величина его могла послужить для определения скорости звука по скорости движения молекул, и обратно. По Стефану величина этого отношения x/u=1/![]() 3=0,577. Гоорвег дал для него число 0,649, а Максвелл в связи с работой Престона вывел для него число 0,745. Эти числа, действительно, могли бы послужить хорошей проверкой для соответствующих теорий, если бы только скорость молекул и скорость распространения звука были более точно известны.
3=0,577. Гоорвег дал для него число 0,649, а Максвелл в связи с работой Престона вывел для него число 0,745. Эти числа, действительно, могли бы послужить хорошей проверкой для соответствующих теорий, если бы только скорость молекул и скорость распространения звука были более точно известны.

Можно смело утверждать, что в течение последних столетий измерения распространения скорости звука никогда не прекращались, и, тем не менее, никогда еще не удалось придти к достаточно точным и надежным результатам. В 1868 г. Реньо снова произвел длинный ряд измерений скорости звука и получил очень точные числа, но вместе с тем он получил такие результаты, которых нельзя было безоговорочно принять. Для этих опытов Реньо использовал длинные газо- и водопроводные трубы; на одном конце трубы звук вызывался пистолетным выстрелом, а на противоположном конце приход звуковых волн отмечался колебанием каучуковой мембраны, натянутой на отверстии трубы. При многих опытах входное отверстие тоже закрывалось каучуковой пластинкой тотчас же после выстрела, и тогда нередко наблюдалось отражение звука до десяти раз. Время, какое требовалось для прохождения звука по трубе вперед и назад, определялось с помощью камертонного хронографа Кенига. Опыты дали ожидаемые результаты, что скорость распространения звука не зависит от давления, что в различных газах она изменяется соответственно корню квадратному из плотности; но вместе с тем они дали и неожиданный результат, что скорость возрастает с силой звука. Для средней скорости распространения звука в сухом воздухе при 0°, исчисленной с момента выстрела и до того момента, когда сила звука настолько уже ослабела, что звук перестает влиять на самую чувствительную мембрану, Реньо получил число 330,6 м. В двух сериях опытов на открытом воздухе, где звук производился пушечными выстрелами с расстояний в 1280 и 5445 м, определились скорости в 331,37 и 330,7 м, откуда Реньо снова сделал заключение об уменьшении скорости звука с уменьшением его силы. Благодаря этим опытам, из которых определилось число, значительно отклоняющееся от выводов прежних измерений, дававших в большинстве случаев число, близкое к 332 м, вопрос о скорости звука опять стал проблематичным.

А. Кундт, который в 1866 г. открыл новый способ демонстрирования звуков с помощью пыльных фигур и применял его для определения скорости звука, использовал теперь этот косвенный метод для проверки результатов, полученных Реньо. Если приводить в сильное звучание воздух в стеклянных трубках, закрытых с одного конца подвижным поршнем, то в них благодаря отражению образуются стоячие волны, заставляющие расположиться легкий порошок, насыпанный в трубке, правильными кольцами или полосами. Эти пыльные фигуры выявляют узловые линии стоячих колебаний и дают, таким образом, возможность точно измерить длину волны, с помощью которой, после установления высоты тона или числа колебаний данного звука, обычным образом можно вычислить скорость распространения звука. Устроив прибор, который давал возможность наполнять трубку различными газами, и, устранив всякое влияние на нее внешних колебаний воздуха, Кундт при помощи этого прибора пришел к следующим выводам: 1) скорость звука в воздухе в трубках уменьшается с диаметром последних и начинает заметно отличаться от скорости его на открытом воздухе, когда диаметр трубки становится меньше 1/4 длины волны тона, примененного при опыте; 2) в узких трубках при шероховатости внутренней их поверхности скорость звука уменьшается; 3) влияние силы звука, равно как и способа его получения, не может быть доказано, если только отвлечься от скорости первой волны; 4) в широких трубках скорость звука не зависит от давления, а в узких — при повышении давления скорость увеличивается; 5) все наблюденные изменения скорости происходят вследствие трения и, в особенности вследствие теплового обмена на стенках трубки. При 100° скорость звука равна v0![]() b>(1+100a), где v0 представляет собою скорость при 0°, a a — коэффициент расширения воздуха. Эти данные Кундта, даже там, где они расходятся с результатами Реньо, хорошо согласуются с полученными около того же времени теоретическими выводами Кирхгофа. Определенное расхождение между последними и экспериментальными результатами Кундта имеется только по вопросу о влиянии диаметра трубок, но их Кундт объясняет частью ошибками наблюдения, частью влиянием примененного порошка на движение в трубках.
b>(1+100a), где v0 представляет собою скорость при 0°, a a — коэффициент расширения воздуха. Эти данные Кундта, даже там, где они расходятся с результатами Реньо, хорошо согласуются с полученными около того же времени теоретическими выводами Кирхгофа. Определенное расхождение между последними и экспериментальными результатами Кундта имеется только по вопросу о влиянии диаметра трубок, но их Кундт объясняет частью ошибками наблюдения, частью влиянием примененного порошка на движение в трубках.
При измерении скорости звука на открытом воздухе на точность результатов вредно влияло изменчивое состояние атмосферы, а при измерениях в трубках — влияние самих трубок. Отсюда явилась потребность произвести измерение скорости звука на небольших расстояниях в возможно закрытых помещениях. Соответствующий метод, так называемый метод совпадения звуков, предложил уже в 1854 г. И. Босша. Если в цепь гальванического тока ввести два электромагнитных звонка и наладить их таким образом, чтобы в то время, когда они стоят вплотную рядом, их удары происходили одновременно, и если затем с одним из этих звонков удаляться от другого, то их звучание будет снова слышно одновременно лишь в том случае, когда звук будет проходить расстояние, разделяющее оба колокольчика, как раз за промежуток времени, протекающий между двумя или несколькими ударами. Отсюда по данным о расстояниях, проходимых звуками за определенное время, уже легко вычислить скорость их распространения даже в пределах комнаты, если последняя достаточно велика. В 1862 г. Кениг устроил прибор для практического осуществления этого метода, однако для совершенно точных измерений он оказался непригодным. Наконец, в 1877 г. Акос Чатмари получил несколько видоизмененным методом для скорости звука в сухом воздухе при 0° число 331,57 м.
В 1874 г. Тиндаль опубликовал интересные наблюдения о совершенно различном распространении звука в воздухе в различных направлениях. Он нашел, что акустическая прозрачность совершенно не зависит от оптической, и приписал акустическую непрозрачность, главным образом, содержащемуся в воздухе водяному пару или смеси его с воздухом. Около того же времени Осборн Рейнольдс пришел к выводу, что туман также ослабляет звук, и объяснил это явление трением колеблющегося воздуха о менее подвижные и, следовательно, относительно покойные частицы воды. Генри и Дюан на основании своих опытов пришли к заключению, что распространению звука всего больше препятствуют различия температур и вызываемые ими воздушные токи и изменения плотностей. В полном согласии с этим последним мнением В. Жэкс полагал, что причина акустических недостатков многих больших аудиторий заключается не только в их пространственных соотношениях, но также в неблагоприятных воздушных течениях, вызываемых особыми местными температурными условиями, и подтвердил свое мнение интересными опытами.