До конца XVIII в. появилось уже множество отдельных работ по акустике. Исследования аккорда и диссонанса, измерения скорости звука, математические выводы форм колеблющихся струн — принадлежали в различное время к числу излюбленных занятий физиков. Во второй половине этого столетия Даниил Бернулли и Эйлер изучали колебания стержней, Эйлер и Риккати колебания натянутых перепонок. Даниил Бернулли, Эйлер, Ламберт, Риккати занимались подробными исследованиями звучащих труб. Лагранж тоже опубликовал свои знаменитые акустические работы в Туринских мемуарах. Однако исчерпывающей, систематической разработки, какая, например, не раз выпадала на долю механики или оптики, акустике все еще недоставало. Подобная всеобъемлющая разработка акустики, как особой и самостоятельной дисциплины физики, была впервые произведена Хладни, «отцом акустики».

Все, что до тех пор было сделано в акустике, принадлежало либо музыкантам, интересовавшимся музыкальными тонами и инструментами также и с теоретической стороны, либо математикам, смотревшим на акустические проблемы, как на интересные математические задачи. Акустические явления сами по себе, если они не возбуждали музыкального или математического интереса, не были еще, за весьма немногими исключениями, предметам исследования. Хладни первый предпринял опытное исследование всей области звука, и первый создал экспериментальную акустику. Братья Вебер отдают ему в этом отношении полную справедливость, предпосылая своему известному «Учению о волнах» (1825 г.) следующее посвящение: «Нашему высокочтимому другу Хладни, основателю опытной акустики, изобретателю нового рода музыкальных инструментов, первому исследователю упавших на землю метеорических масс».
Сам Хладни в предисловии к своему главному труду, вышедшему в свет в 1802 г. в Лейпциге под заглавием «Die Akustik», считает новым и лично ему принадлежащим: план сочинения, «при котором внимание обращено не исключительно или предпочтительно, как это обычно делалось, на струны, но на все возможные виды звучащих тел в одинаковой степени»; исследование колебаний дисков, колоколов, колец и камертонов; открытие продольных колебаний струн и стержней, а равно применение их к определению скорости звука в твердых телах; открытие вращательных колебаний стержней, открытие законов звучания горящего водородного пламени; определение числа колебаний непосредственным счетом; определение скорости звука в различных газах и, наконец, изобретение эуфона и клавицилиндра. Мы увидим впоследствии, что эти притязания более чем оправдываются фактами.
«Большинство авторов определяет высоту музыкальных звуков (так было во времена Хладни) по соответствующим им длинам струн». Хладни обращает внимание на необходимость заменить длины струн, пригодные лишь как относительные числа, абсолютными числами колебаний звуков. Для определения числа колебаний звука «тонометром», или «счетчиком звука», ему служил стержень, имевший форму параллелепипеда, длиною в 2 локтя, шириной 1/2 дюйма и толщиною в 1 линию, пропущенный для придания равномерности по всей длине через каток. Этот стержень он закреплял в станке, снабженном винтом, таким образом, что он давал очень медленные колебания, которые, правда, не воспринимались ухом как музыкальный тон, но которые можно было легко видеть и подсчитать. Для определения высоты данного звука при помощи этого прибора нужно было настроить последний на тот же тон, передвинув его надлежащим образом в станке, и вычислить число колебаний по следующей пропорции: числа колебаний одного и того же стержня обратно пропорциональны квадратам длины колеблющихся частей.
Несмотря на то, что великие математики половины XVIII века изучали с большим интересом и терпением формы колеблющихся струн, Хладни именно в этой области удалось получить много нового. Упомянутые математики, сосредоточив все свое внимание на возможных формах колеблющихся струн, постоянно принимали, что отдельные части струны колеблются перпендикулярно к длине струны. Хладни указал на возможность таких колебаний, при которых отдельные части струны не выходят из направления струны. Он сообщил о своем открытии в первой работе «Neue Entdeckungen über die Theorie des Klangers» (Leipzig 1787) («Новые открытия в области теории звука») и подробнее в 1792 г. в журнале «Berliner musikalischen Monatschrift», а также в ряде последующих монографий. Он установил, что одна и та же струна дает различные тоны в зависимости от того, проводят ли по ней смычком нормально к ее направлению или же под возможно острым углом; последнее достигается еще лучше, если струну, натертую канифолью, тереть суконкой или пальцем вдоль ее длины. В первом случае отдельные части струны колеблются перпендикулярно к ее направлению, в последнем случае — в том же самом направлении. Первого рода колебания Хладни назвал поперечными, а открытые им колебания второго рода продольными 1. Когда струна издает свой наиболее низкий продольный тон, основной тон, все части ее колеблются одновременно в одном и том же направлении. Но струна может так же, как при поперечных колебаниях, делится на части и издавать обертоны. При первом обертоне, где по середине струны находится узел колебания, частицы в обеих половинах движутся в противоположном направлении, т. е. все одновременно по направлению к узлу или же прочь от него и т. д. Продольные тоны всегда значительно, иногда на несколько октав выше поперечных на той же струне; определенного соотношения между обоими родами тонов в общем случае нельзя было установить. Скорости продольных колебаний обратно пропорциональны длинам струн; толщина и степень натяжения последних странным образом не оказывают влияния на скорость, зато материал влияет самым решительным образом. На стержнях обертоны продольных колебаний получаются еще легче, чем на струнах. Для получения основного тона всего целесообразнее вставить стеклянную палочку одним концом в винтовой станок, а другой конец потереть мокрым сукном, посыпанным мелким песком или пемзой. Для получения первого обертона стоит только прикоснуться пальцами к середине палочки; он будет, разумеется, октавой основного тона. Хладни приводит продольные тоны двухфутового прута для 26 веществ, между которыми находятся китовый ус, олово, разного рода дерево и даже глиняный чубук.
На стержнях Хладни открыл еще третий род колебаний, описанный им в 1799 г. во втором томе журнала «Schriften der Cesellschaft naturforschender Freunde», издававшегося в Берлине. Эти «вращательные колебания» он получал на очень гладких цилиндрических стержнях при трении их справа налево во вращательном направлении. И в данном случае стержень, смотря по тому, как его держали, делился, как и при продольных колебаниях, на части; законы колебания, в общем, оказались здесь те же, что и для продольных, но только тоны при прочих равных условиях оказались на квинту ниже. Это наблюдение, согласно которому числа колебаний обоих видов колебательных движений должны относиться друг к другу, как 3:2, было подтверждено последующими опытами. Мунке получил из своих опытов для этого отношения число 1,6 (соответствующее большой сексте). Пуассон вывел из теоретических соображений, основанных на законах упругости, величину 1/2?10 или 1,5811. По Веберу последние числа довольно близко подходят к результатам его собственных опытов.
Исследование колебаний прямых стержней Хладни распространил и на изогнутые стержни (черт. 4). Он показал, что на камертоне, когда он издает свой наиболее низкий тон, находятся два колебательных узла на близком расстоянии по обе стороны ножки и что тон его приблизительно на сексту ниже основного тона поперечного колебания свободного стержня. Хладни исследовал также колебания стержней, изогнутых в кольца, а равно и колоколов, причем экспериментально подтвердил некоторые из теоретических выводов Эйлера (Act. Petr. 1779) и Головина (Act, Petr. 1781).

Больше всех перечисленных выше открытий обратили на себя внимание работы Хладни над колеблющимися пластинками и открытие им звуковых фигур. Первое сообщение о них появилось также в его первом сочинении «Entdeckungen über die Theorie des Klanges» (1787). В своей «Акустике» 1802 г. он изложил этот вопрос более подробно, и, наконец, дополнительные данные он привел в позднейшем своем сочинении «Neue Beiträge zur Akustik» (Leipzig 1817) («Новые исследования по акустике»). Получение звуковых фигур так хорошо известно и так подробно изложено в каждом почти учебнике физики, что я могу здесь на них не останавливаться. Предпочитаю привести взамен этого собрание чертежей из «Акустики» Хладни (черт. 5), которое полнее обычно встречающихся в учебниках; и все-таки здесь представлена только небольшая доля чертежей, вычерченных самим Хладни. В 1787 г. появилось уже 138 изображений квадратных и круглых пластинок; «Акустика» 1802 г. содержит 190 рисунков звуковых фигур, а к 1817 г. к прежним прибавилось еще много новых. Какие ожидания Хладни возлагал на свои звуковые фигуры, об этом можно судить по начальным строкам его сочинения «Entdeckungen über die Theorie des Klanges». «Упругие колебания струн и стержней, где приходится иметь дело с несколькими отдельными кривыми линиями, были уже вычислены различными исследователями с такою точностью и тонкостью, что о них, пожалуй, можно сказать очень мало нового. Напротив, истинный состав звука таких тел, относительно которых нужно принимать в расчет упругие колебания целых плоскостей в нескольких измерениях одновременно, находится еще в полном мраке, так как по этому вопросу не существует ни вычислений, согласных с опытом, ни точных наблюдений. Мне удалось найти средство, при помощи которого всевозможные виды звуков подобных тел, без примеси других, можно не только слышать, но и видеть; и потому я надеюсь сообщением об этих моих наблюдениях дать хоть несколько правильных указаний для более точного исследования этого мало разработанного отдела механики. Я уверен вместе с тем, что неполноту моих замечаний извинит всякий, знающий по своему личному опыту, с какими трудностями приходится на каждом шагу встречаться тому, кто ставит себе целью изучение природы по непроторенным путям».
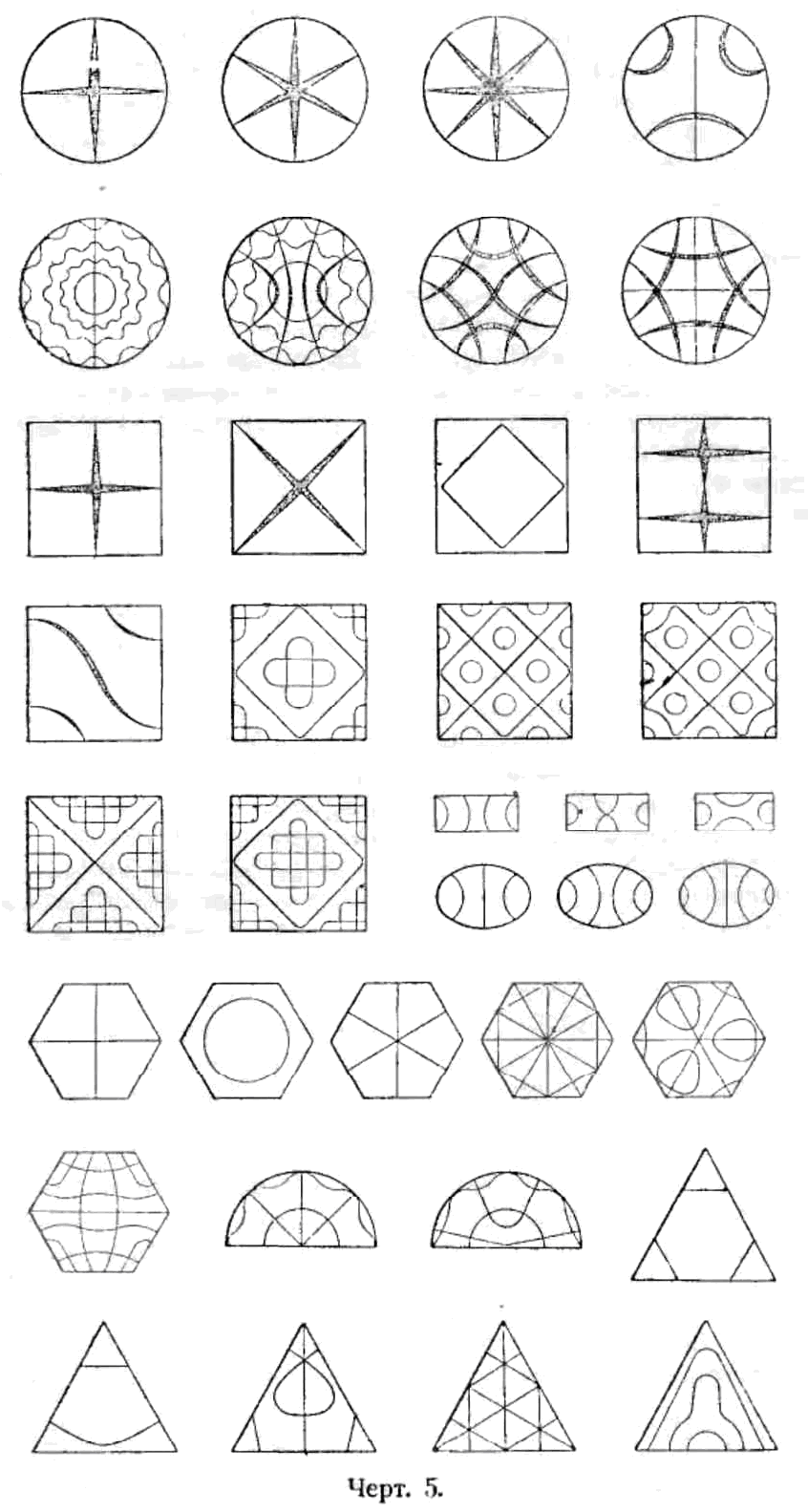
Степень интереса, по крайней мере, со стороны ученой публики, вполне соответствовала ожиданиям. Лекции и опыты Хладни возбуждали всеобщий и живой интерес; ученые и любители с увлечением повторяли его опыты. Когда Хладни в 1809 г. представил свои фигуры членам Французского национального института, все, и в особенности Лаплас, смотрели на них с изумлением. Наполеон пожелал видеть повторение этих опытов в Тюильерийском дворце и отпустил Хладни 6000 франков для перевода его «Акустики» на французский язык.
Тем не менее, нельзя не признать, что эти открытия не принесли ожидаемой пользы для теории звука; с одной стороны, потому, что они оказались непосредственно приложимыми к одному только частному случаю колеблющихся пластинок; а с другой — вследствие того, что теория не знала, что ей собственно делать с этими опытными данными. Еще в 1787 г. Яков II Бернулли (Nov. Act. Petr., V, 1787) пытался теоретически вывести форму некоторых звуковых фигур, для чего он рассматривал прямоугольную пластинку как сетчатую ткань из волокон, пересекающихся под прямым углом. Однако Хладни показал, что полученные таким путем результаты расходятся с опытом. После демонстраций, сделанных Хладни перед Французским институтом в 1809 г., последний назначил премию в 3000 франков за аналитическое решение этой задачи. Пришлось, однако, дважды повторить приглашение на конкурс и только в 1816 г. выдать, наконец, премию Софии Жермен за единственную представленную работу, заключавшую в себе несколько верных дифференциальных уравнений и несколько новых исследований. Работы Пуассона над этой проблемой дали весьма немного, и только в 1883 г. Уитстон дал теорию, согласно которой могли быть правильно выведены хотя бы простейшие звуковые фигуры.
Хладни принадлежат также первые опыты по определению скорости распространения звука в газах. Помимо почти невыполнимого непосредственного измерения для определения этой скорости существовали два пути. Со времени работ Даниила Бернулли в 1762 г. было известно, что в открытых органных трубах узел колебаний лежит по середине, а пучности колебаний на концах трубы и что, следовательно, когда труба издает свой основной тон, то длина волны этого тона вдвое больше длины трубы; при закрытых же трубах длина волны превосходит длину трубы в четыре раза. А так как уже Ньютон доказал, что скорость распространения всех колебаний вообще равна произведению числа колебаний на длину волны, то, очевидно, скорость распространения звука в газе, наполняющем трубу, может быть легко вычислена из длины трубы и числа колебаний ее тона. Хладни применял для этой цели открытую оловянную органную трубу, укрепленную на стеклянном колоколе, погруженном в воду открытым концом. С колоколом сообщался животный пузырь, содержащий исследуемый газ. Для более точного сравнения опыт всегда начинался с атмосферного воздуха и издаваемый в последнем тон тщательно определялся при помощи монохорда. Второй путь быстрее приводит к цели. По Ньютону скорость распространения волн в различных упругих средах обратно пропорциональна квадратным корням из удельных весов соответствующих газов. Так как удельные веса газов и скорость распространения звука в воздухе уже известны, то из этих данных легко вычислить соответствующие скорости распространения звука в газах. Результаты, полученные Хладни обоими путями, указаны в следующей таблице:
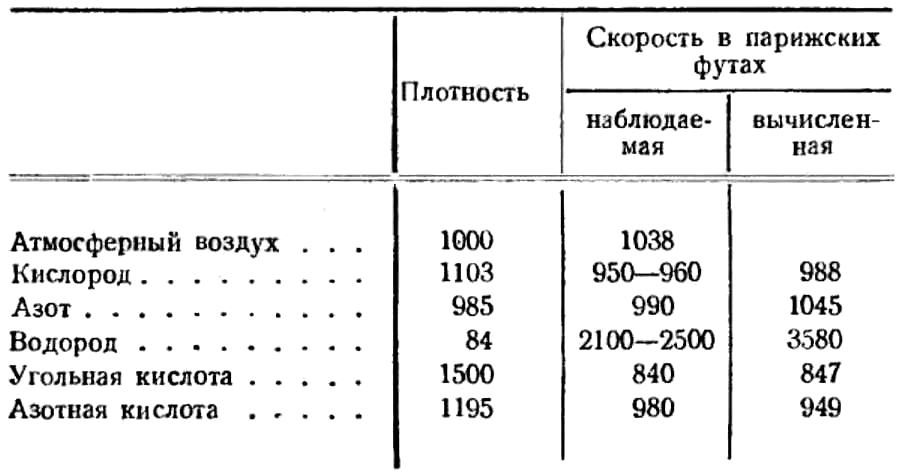
Эти результаты дают отклонения, которые не могут быть объяснены одною только неточностью в измерениях. Бенценберг нашел при собственных опытах, а также в измерениях Керби и Меррика, предпринятых по тому же плану, приблизительно те же отклонения от величин, исчисленных по закону Ньютона. Гильберт объяснял эти отклонения трудно устранимой засоренностью газов и ссылался при этом на то обстоятельство, что угольная кислота, которую всего легче получать в чистом виде, дает наиболее согласные результаты. Различная степень влажности газов могла, по его мнению, тоже быть одной из причин неточности. Однако опыты новейшего времени показали, что отклонения эти не случайны, а зависят главным образом от влияния стенок звучащих труб.
И все-таки эти отклонения не были еще настолько удивительны, как неустранимые никакими усилиями расхождения между наблюденной скоростью звука на открытом воздухе и величиной ее, вычисленной для этого случая Ньютоном. Чем больше и тщательнее производились измерения скорости звука на воздухе, тем очевиднее становилось, что ньютоново число 797 англ. футов в секунду ни в каком случае не может быть правильным; вместе с тем не удавалось найти ни причины этого расхождения, ни какой бы то ни было ошибки в выводах Ньютона. Еще в недавнее время, в 1778 г., немецкие ученые Кестнер (Kästner) и Майер (J. Т. Mayer) снова тщательно определили скорость звука в воздухе и получили результат, очень близкий к полученному в 1738 г. Парижской академией, а именно 1034—1037 париж. футов. Хладни приводит следующие объяснения для этого загадочного расхождения: 1) воздух содержит посторонние примеси, увеличивающие его вес, но не упругость (Lambert, Ber. Mém., 1798); 2) скорость воздушных колебаний увеличивается от ударов последующих колебаний (Euler, Conjectura phys., Berlin 1750, от этого положения он позднее отказался как от неверного, «De la propagation du son», 1759); 3) более сильные воздушные толчки воздуха распространяются быстрее, чем малые, которые одни только и являются объектом теоретических расчетов; 4) упругость воздуха изменяется не вполне пропорционально его плотности (Lagrange, Tur. Misc., II); 5) воздух, как смесь азота и кислорода, производит иные колебания, чем простые газы. Последнее предположение Хладни считает наиболее вероятным и пытается даже объяснить изменение звука духовых инструментов в наполненных людьми залах изменением состава воздуха в этих помещениях. Неудовлетворительность всех этих попыток явствует уже из того, что ни один из исследователей не мог указать основания для теоретического вывода наблюденных чисел; поэтому все они и отпали тотчас же после того, как Лаплас дал правильное объяснение, сохранившее свою силу до наших дней.
По свидетельству Ле-Конта Лаплас уже в 1800 г. заметил, что повышения и понижения температуры, связанные со сгущением и разрежением воздуха при звуковых волнах, изменяют упругость воздуха в большем отношении, чем его плотность, к что это обстоятельство должно повышать скорость звука. Свою мысль он тогда же сообщил Био, который в 1802 г. в «Journal de Physique» попытался применить ее на деле и произвести перерасчет — впрочем, не совсем правильно с математической стороны, как это в 1808 г. доказал Пуассон. Однако и самому Лапласу пришлось довольно долго поработать над этим вопросом, пока он получил возможность опубликовать точный результат своих исследований, а вместе с тем и решение настоящей задачи: «Скорость звука равна скорости ее, данной ньютоновской формулой, помноженной на квадратный корень из отношения удельной теплоемкости воздуха при постоянном давлении к удельной теплоемкости его при постоянном объеме». К сожалению, как раз величина этого отношения удельных теллоемкостей была в то время настолько неточно определена, что судить о правильности этого закона по верности результата было невозможно. Поэтому вплоть до наших дней не было недостатка в физиках, которые не признавали правильности теории Лапласа и пытались дать лучшее объяснение. Венценберг, произведший в декабре 1809 г. и июне 1811 г. близ Дюссельдорфа много опытов по определению скорости распространения звука и получивший для температуры 0° С широко распространенное число 1027 париж. футов, счел это число слишком высоким для того, чтобы оно могло быть отнесено за счет теплоты, развивающейся при сжатии воздуха. Мейкле в 1829 г. высказал предположение, что если теплота сжатия действительно ускоряет распространение звука, то сильные звуки должны распространяться скорее слабых. Ричи утверждал, что теплота совершенно не может влиять на скорость звука, так как сгущенные части волн распространяются не быстрее разреженных. Мун допускал, что последнее имеет место, но наш слух способен воспринимать только сгущенные волны. Поттер укоризненно отметил, что Лаплас мог с одинаковым основанием вывести заключение о замедлении звука, как и об ускорении его, так как при волнообразном движении воздуха образуются и тепло и холод. По мнению Чаллис, развивающиеся тепло и холод должны уравновешиваться; сверх того, повышение температуры в действительности наблюдается только в трубах, на открытом же воздухе избыточное тепло должно быстро рассеиваться вследствие излучения. Против последнего мнения выступил Стокс, указавший, что изменения плотности происходят настолько быстро, что подобное выравнивание тепла и холода не может иметь места.
Однако постепенно все возражения против теории Лапласа стали умолкать, и Ле-Конт в упомянутом выше исследовании доказал, что эта теория близко согласуется с опытом, если только положить в основание новейшие точные величины для входящих в расчеты физических постоянных. Действительно, приняв (по Реньо) удельный вес ртути по отношению к воздуху равным 7990,044388, ускорение силы тяжести (по Бэли) равным 9,80942005 м, отношение удельных теплоемкостей (по Массону) 1,41, он для скорости распространения звука получил 332,43 м — результат, хорошо согласующийся со всеми полученными в новейшее время данными наблюдения.
Распространение звука в жидкостях, которое раньше считали невозможным ввиду недостаточной их упругости, Хладни считал вполне доказанным. Он обращает при этом внимание, что Нолле и Мушенбрек установили независимость распространения звука от заключающегося в воде воздуха, доказав это опытами. Однако измерение этой скорости не было предпринято ни им самим, ни его ближайшими преемниками.
Скорость распространения звука в твердых телах впервые попытался определить в восьмидесятых годах XVIII века Вюнш. Он соединил 36 планок длиною по 24 фута каждая таким образом, что они составили катеты прямоугольного треугольника, гипотенуза которого оставалась открытой. Когда затем помощник ударял молотком по концу одного из катетов, то Вюнш на конце другого катета тотчас же слышал стук, передававшийся через дерево мгновенно, тогда как по воздуху звук доходил на 1/2 сек. позже. На основании этих опытов он пришел к выводу, что через твердые тела вообще звук передается мгновенно. Хладни в 1797 г. совершенно иным путем пришел к гораздо лучшему результату. Так как продольные колебания твердых тел должны происходить, во всяком случае, аналогично продольным колебаниям воздуха в открытых органных трубах, то для первых, подобно вторым, длина волны основного тона должна равняться удвоенной длине звучащего стержня. Таким образом, из наблюдаемой длины стержня получается длина волны, из высоты тона — число колебаний, а произведение этих двух величия должно дать скорость распространения звука в данном стержне. Этим путем Хланди получил для различных веществ следующие относительные числа скорости звука в них по отношению к скорости его в воздухе: олово 7,5; серебро 9; медь 12; железо 16,7; стекло 16,7; дуб 10,7; буковое дерево 12,5; липовое дерево 15; еловое дерево 16 и т. д. Эти числа очень близко подходят к новейшим данным, полученным путем непосредственного наблюдения.
Если до сих пор в лице Хладни мы видели человека, который был исключительно счастлив по части открытий и был непогрешимым экспериментатором, то теперь нам остается указать на некоторые вопросы, при разрешении которых он не мог добиться полного успеха.
По свидетельству Мунке Брайан Гиггинс впервые в 1777 г. наблюдал звуки водородного пламени в стеклянной трубке, но опубликовал свои исследования только в 1797 г. в журнале Никольсона, после того, как его уже успели опередить на этом пути Делюк в своих «Nouvelles idées de météorologie» (1787), Гермбштедт («Crell's chem. Ann.», 1793) и Тромсдорф («Erfurter Gelehrte Zeitung», 1794). Последний считал, что причину этих звуков невозможно вполне объяснить: они могут происходить вследствие того, что под влиянием пламени образуется вакуум, в который постоянно устремляется наружный воздух; причиной их могут служить также нагревание стекла изнутри горячим воздухом и охлаждение его снаружи окружающей атмосферой, вследствие чего и стенки трубки должны приходить в колебание. Граф Мусин-Пушкин полагал, что звучание в данном случае происходит от постоянных взрывов гремучего газа. Шерер присоединился к этому мнению с тем лишь отличием, что, по мнению Пушкина, от этих взрывов приходит в колебание один воздух, а, по мнению Шерера и стеклянная трубка. Хладни в 1795 г. 2 указал, что последнее мало вероятно, так как прикосновение к стеклу и даже обертывание последнего сукном не препятствуют образованию звуков; гораздо естественнее, по его мнению, допустить, что воздух в стеклянной трубке приводится притекающим снизу атмосферным воздухом в такие же продольные колебания, какие имеют место в органных трубах, и трубка должна при горении водородного пламени издавать тот же тон, как при вдувании в нее воздуха мехами. То обстоятельство, что пламя других газов не издает звуков, происходит вследствие недостаточного притока газа, а также вследствие менее равномерного горения. Авторитет Хладни на долгое время обеспечил этой гипотезе общее признание.
Наравне с химической гармоникой, общий интерес возбуждало в этот период времени другое уже известное акустическое явление, а именно: гармоническое звучание натянутых струн при ветре, для которого были придуманы более причудливые объяснения, чем для первого.
После того как около половины XVIII века шотландский музыкант Освальд натянул в гармоническом порядке несколько струн в длинном ящике с резонансом и при ветре стал получать при его помощи «разнообразие восхитительных тонов, превосходящее всякое описание», патер Вентан в м. Беркли близ Базеля случайно открыл, что и одна струна способна издавать различные тоны. У него во дворе зачем-то была подвешена длинная железная проволока, и он заметил, что когда последнюю натягивали параллельно полуденной линии, то при каждой перемене погоды она издавала различные звуки; если же ее натягивали по направлению с востока на запад, звуков не было. Медные проволоки не издавали звуков ни при каких условиях. Хладни отверг возможное в данном случае предположение о связи звуков воздушной арфы с магнетизмом проволоки и обратил внимание на то, что направление проволок с севера на юг объясняется, вероятно, местными условиями и преобладающим направлением ветра с запада на восток. Между тем, М. Юнг уже около двух десятилетий до того дал подробное и удовлетворительное объяснение этого музыкального инструмента. Исследуя последний, он снимал с него струны одну за другой и установил, что даже при наличии одной струны последняя издает гармонические звуки. Он доказал, кроме того, на опыте, что ветер составляет единственную причину колебания струн и разнообразия звуков. Дело в том, что удары ветра редко приходятся против самой середины струны арфы, а чаще всего против различных мест, причем струны делятся на несколько колеблющихся частей, и наряду с основным тоном, бывают слышны и обертоны. Это объяснение, к которому присоединялся и Хладни, не могло быть оценено по достоинству в то время, так как сущность обертонов (или побочных тонов, как их тогда называли) не была еще тогда выяснена.
Фридрих Готлиб фон-Буссе в конце XVIII в. был еще склонен отрицать возможность того, чтобы при звучании какого-либо тона одновременно звучали и другие, более высокие. Хладни, правда, отметил, что на струнах, несмотря на все предосторожности, почти всегда одновременно бывает слышно слабое звучание третьего и пятого гармонических тонов и что в духовых инструментах, органных трубах и звучащих стержнях как будто тоже постоянно бывает слышен ближайший обертон. Но наряду с этим он указывает, что, по крайней мере, на струнах удается получать и чистые тоны, если только заглушать их в надлежащих местах: Затем он решительно восстает против мнения тех, которые утверждают «будто тон, в сущности, представляет собою аккорд, и что тем самым он и отличается от простого стука». Вместе с тем, по его мнению, обертоны несущественны и примешиваются к основному тону только случайно. С этой точки зрения он идет дальше: так как обертоны несущественны и часто бывают даже негармоничны, то Рамо, Жамар, Зульпер, Эркслебен и др. совершенно неправы, объясняя основные законы всякой гармонии существованием обертонов. Признаком консонирующих и диссонирующих интервалов остается, таким образом, для Хладни (как и для акустиков-математиков — Эйлера и др.) только большая или меньшая простота отношения их чисел колебаний; и Хладни в предисловии к своей «Акустике» (стр. XI) прямо вменяет себе в заслугу, что он уничтожает предрассудок, согласно которому консонансы и диссонансы интервалов обыкновенно ставятся в зависимость от созвучия высших тонов. К сожалению, оттеснив, таким образом, обертоны в область случайностей, Хладни лишил себя возможности дать какое бы то ни было правдоподобное объяснение для различных оттенков тона. В своей «Акустике» он прямо заявляет (стр. 218): «Подобно тому, как до сих пор ничего не известно о природе различных изменений звука, так же остается неизвестным, каким образом в воздухе распространяются разнообразные звуковые оттенки (тембры). Л. Эйлер» (Mém. Berl., 1765, а также «De motu aéris in tubis») считает вероятным, что эти видоизменения и сочетания тонов обусловливаются ничтожными различиями в степени уплотнения воздушных частиц и скорости, с которой каждая выводится из своего первоначального положения».
Изобретенные Хладни новые музыкальные инструменты, эуфон и клавицилиндр, внутреннее устройство которых он держал в секрете до 1821 г., хотя и возбудили на первых порах большой интерес, но не удержались в милости у музыкантов и публики; вероятно, потому, что тоны деревянных, стеклянных и металлических пластинок, входивших в состав этих инструментов, были слишком слабы и однообразны. Они выполнили свое предназначение, поскольку дали на первых порах великому специалисту в области акустики средства к жизни и помогли создать необходимые условия для его плодотворных научных работ, и вместе с ним сошли в могилу.