Учение о волнообразном движении имело очень своеобразную судьбу вплоть до 1825 г. Водяные волны наблюдались с интересом еще до Аристотеля, и интерес к ним не исчезал и потом. Но до опытного исследования их и до опытной теории волн, — если не принимать в расчет единичных более специальных указаний, обративших на себя мало внимания, — дело не доходило. Волнообразное движение и стоячее колебание воздуха, струн и т. п., которые мы ощущаем, как звук, составляло со времен Ньютона одну из любимых тем наиболее выдающихся математиков; их упрощенные исходные положения, принятые в основание математической дедукции, так мало соответствовали сложным условиям действительности, и согласие их выводов с опытными фактами было так незначительно, что ценность их работ оказалась настолько же сомнительной для физики, насколько они были безупречны с математической стороны. Но когда трудами Френеля волновая теория эфира была построена на столь прочных основаниях, наступила пора сделать и для весомой материи то, что удалось для невесомой: перед экспериментальной физикой возникла настоятельная задача изучить путем наблюдения волнообразное движение хотя бы в такой мере, чтобы создать необходимую основу для последующего развития теории. Эта задача была блестяще и в законченном виде выполнена братьями Вебер в их классическом сочинении «Wellenlehre auf Experimente gegründet, oder über die Wellen tropfbarer Flüssigkeiten mit Anwendung auf die Schall- und Lichtwellen (Leipzig 1825) («Учение о волнах, основанное на опыте, или о волнах капельножидких тел с применением к звуковым и световым волнам»). Мы постараемся воздать должное значению этой работы, изложив здесь вкратце ее содержание.
Существует два вида колебательных движений: поступательное и стоячее. Поступательное равнозначно с волнообразным движением. Волнообразное движение принадлежит к числу наиболее распространенных явлений природы, тогда как стоячие колебания замечены до сих пор лишь на звучащих телах. Для возбуждения стоячих колебаний есть два пути: либо все части тела приводят в такое положение, что все они одновременно и с одинаковою силой стремятся выйти из него,— это — путь, которым следовали до сих пор математики, но которому редко следует природа, — либо направляют навстречу друг другу с одинаковой силой много одинаково широких волн, ширина которых составляет какую-либо часть колеблющейся линии или поверхности. (На этот последний путь мы обращаем особенно внимание).
Франклин первый удовлетворительно объяснил образование водяных волн ветром. По его мнению, воздух прилипает к воде, поэтому ветер, действуя на поверхность последней, гонит воду перед собою. Но так как при этом верхние частицы воды увлекают за собою нижние, то движение воды и воздуха становится все более медленным, пока напор последующих частиц воздуха не оторвет предшествующих от воды. После этот напряжение постепенно ослабевает, и игра начинается вновь. Согласно теории Веберов, подобным трением между водою и воздухом вызываются лишь самые маленькие волны (рябь) на поверхности больших волн; последние же производятся исключительно ударом или давлением ветра на воду. Постоянное затем нарастание этих волн зависит от четырех причин: 1) от продолжающегося действия ветра на те части волны, которые перемещаются в его направлении; 2) от слияния нескольких волн, идущих в одном и том же направлении, в одну волну; 3) от давления, производимого каждой волною на предшествующую и последующую волну; наконец, 4) от перекрещивания волн, идущих в противоположных направлениях. Как будет показано дальше, в передней половине волны все частицы находятся в восходящем движении, в задней половине — в нисходящем. Волна обращена к ветру больше задней половиной своей, поэтому здесь ветер сильнее гонит вниз частицы ее, тогда как подъему передней половины волны он мало мешает, ибо здесь он действует под острым углом к волне. С волнами, идущими навстречу ветру, происходит как раз обратное; поэтому волны вообще идут с ветром и суммируются в его направлении. Всякая волна при своем передвижении возбуждает на оставляемом ею месте новую волну; эта новая волна, передвинувшись на свою ширину, в свою очередь, порождает позади себя новую волну; и таким образом за первой волной может последовать 20—40 новых, и все они передвигаются в одном направлении с первой. Таким обратным действием волны на последующие, от которого, между прочим, зависит увеличение волн, объясняется большая правильность в чередовании волн, несмотря на неправильность толчков ветра.
На море часто замечается множество линейных гряд волн, пересекающихся друг с другом под различными углами. В местах пересечения таких гряд образуются, конечно, более высокие волны, исчезающие по мере передвижения гряд и вновь возникающие; оттого кажется, будто волны здесь нисколько не перемещаются, а только поднимаются и опускаются. Кроме того, большие волны, распространяющиеся, как будет показано, быстрее мелких, с виду как будто катятся под поверхностью мелких. От перекрещивания же волн получается их зазубренность. Большие волны могут образоваться лишь при большом протяжении водной поверхности и при значительной глубине.
Поднятие над поверхностью есть лишь результат распространяющегося далеко вглубь внутреннего движения жидкости. Если волна образовалась в глубине, то, дойдя до мелкого места, она быстро нарастает в высоту, передняя ее половина становится более крутою, и волна ломается. С точки зрения этой теории легко объяснить успокоение волнения при выливании на воду масла, что наблюдалось много раз. Масло, быстро распространяясь на поверхности воды, мешает образованию первых волн и усилению или сохранению уже существующих.

Для экспериментального определения формы волн капельных жидкостей и происходящих в волнах отдельных перемещений частиц братья Вебер употребляли устроенную ими ванну, изображенную на черт. 10. Чтобы наблюдать форму поверхности волны, когда ванна наполнена маслом, берут прямоугольный кусок аспидной доски, посыпанной мукою; если же ванна наполнена водою или смесью спирта с водой — такой же кусок матовой стеклянной пластинки. При опускании такой пластинки в ванну параллельно ее продольным стенкам получается линия уровня, которую отмечают чертой. Затем с одного конца в ванну пускают каплю жидкости и, как только первая возвышенная часть волны достигнет середины пластинки, последнюю выдергивают со скоростью, превышающей скорость распространения волны; тогда передняя часть холма волны отпечатывается совершенно правильно. Заднюю часть ее получить уже труднее, — для этого нужно пластинку быстро погрузить в ванну и тотчас же быстро вынуть.
По отношению к своей ширине волны необыкновенно плоски. Чтобы наблюдать пути колеблющихся в волне частиц, братья Вебер наполняли свою ванну мутной водой (из реки Заала возле Галле) с взвешенными в ней мелкими частицами твердых тел и наблюдали движения частью невооруженным глазом, частью при посредстве простого микроскопа с фокусным расстоянием в 31/2 линии. При помощи маленького пружинного циркуля, концы которого помещались между микроскопом и стеклянным боком ванны, они точно определяли размеры путей.
Пути колебаний частиц жидкости, когда последующие друг за другом холмы и долины волн имеют одинаковые или почти одинаковые очертания, представляются совсем или почти совсем замкнутыми, уподобляясь эллипсам, расположенным в вертикальной плоскости. Когда же холмы и равнины не равны, то пути частиц не замкнуты. В первом случае близ поверхности эллипсы походят на круги, по мере углубления они становятся все более и более плоскими и, наконец, превращаются в прямые горизонтальные линии. При этом все размеры уменьшаются; более скорое уменьшение вертикальных размеров вызывается, по-видимому, дном сосуда. У самой поверхности вертикальный диаметр пути частицы равен высоте волны, а горизонтальный диаметр не находится в каком-либо определенном отношении к ширине волны. Частицы одного уровня, расположенные горизонтально по направлению волны, приходят в движение одна вслед за другой, так что в сфере одной волны имеется лишь немного частиц, которые находились бы одновременно в одинаковых точках своих путей; наоборот, частицы, расположенные по вертикали друг над другом, по-видимому, приходят одновременно в соответственные точки своих путей.
За то время, в течение которого частица жидкости описывает весь свой путь, волна, в которой эта частица содержится, перемещается на расстояние своей ширины; поэтому частица в течение данного времени столько раз описывает свой путь, сколько волн проходит через то пространство, в котором она движется.
Скорость распространения волн ни в коем случае не зависит только от их ширины, как утверждали Ньютон, с'Гравезанд, д'Аламбер, а в последнее время и Герстнер, но от всего ее размера, т. е. от ширины и высоты. Только длина волн не имеет непосредственного влияния на их скорость; однако, когда при распространении волн их длина увеличивается, то вместе с тем уменьшается одновременно их скорость и высота, и наоборот. Волны, предоставленные самим себе, имеют свою длину, ширину и высоту таким образом, что первые две величины увеличиваются за счет последней. В волнах упругих жидкостей высота и ширина совпадают в один размер, в толщину. Так как ширина может увеличиваться только за счет высоты, то понятно, что волны упругих жидкостей не могут изменяться в ширине, пока они не переходят в другую среду, что признано и всеми физиками. По этой же причине и скорость этих волн не зависит от их величины, а лишь от упругих сил среды, тогда как волны неупругих жидкостей не зависят от плоскости последних. Все это обусловливается тем, что волны первого рода распространяются по трем направлениям, а волны второго — только по двум. При перекрещивании волн холмы и долины соединяются в более высокие холмы и более глубокие долины, но затем они снова расходятся, принимая прежние размеры и прежние направления. Перекрещивание сопровождается некоторым замедлением, затем прежние скорости восстанавливаются.
Волна, вызванная падением столба жидкости в одном конце ванны, распространяется до другого конца и отражается здесь таким образом, что холм опять предшествует долине, так что по отношению к стенке сосуда обе половины теперь расположены в обратном порядке по сравнению с первой волной. Таким образом, при отражении положение каждой волны изменяется на обратное, хотя отражение вызывается отнюдь не упругостью жидкости, а ее тяжестью. Если в сосуд эллиптической формы налить ртути и затем начать капать ртутью в один из фокусов эллипса, то образуется непрерывный ряд волн, отражающихся в другом фокусе, и тогда на поверхности можно видеть рядом волны во всех тех стадиях, которые последовательно претерпевает одна волна на протяжении времени. Когда волна падает на перегородку с отверстием, она частью отражается, частью распространяется далее; Вебер показал, что при этом, подобно тому, как это имеет место в свете при интерференции, образуются гиперболические линии пересечения, соответствующие интерференционным полосам света.
Так как стоячее колебание есть не что иное, как непрерывно повторяющееся правильное перекрещивание волн, то его легче всего можно воспроизвести, возбуждая через правильные промежутки времени волны одинаковой ширины и отражая их от правильных стенок сосуда таким образом, чтобы холмы и долины перекрещивались между собою дважды или много раз в точках, расположенных симметрично, и чтобы самые высокие и самые низкие точки всех этих перекрещиваний находились на равных расстояниях друг от друга. В таких волнах частицы описывают не замкнутые в себе кривые, но движутся по одному и тому же пути вперед и назад. Стоячие волны, хотя и неправильные, образуются также почти всегда, когда сосуд с жидкостью подвергают длительной встряске.
После такого совершенно оригинального и исчерпывающего исследования волн капельных жидкостей братья Вебер обращаются к рассмотрению волн, применительно к звуку и свету. Однако здесь, отчасти в силу свойств самой проблемы, исследование уже не блещет ни прежней оригинальностью, ни прежней законченностью. Хладни отличал в звучащих телах три вида колебаний: поперечное, продольное и вращательное; но Савар пытался доказать, что такое различение не имеет значения. Еще ранее 1819 г., с целью установить теорию струнных и смычковых инструментов, Савар принялся за более углубленное исследование явлений резонанса. Его замечания о значении резонансного ящика, подструнной рукоятки, кобылки и шейки этих музыкальных инструментов получили большое теоретическое значение. Однако скрипка, построенная по его принципам в форме гробового ящика и встретившая даже некоторое одобрение со стороны комиссии Парижской академии, не побудила скрипичных мастеров отказаться от подражания старым итальянским мастерам и строить свои инструменты на теоретических началах Савара. Вызванные стремлением создать теорию музыкальных инструментов новые исследования Савара о резонансе твердых тел, хотя и дали новые и важные результаты, но сделанные из них выводы опять-таки не встретили полного признания. Для того чтобы определить влияние скрипичной рукоятки, Савар прикрепил к концам длинной доски в поперечном направлении две других дощечки меньшей величины. Когда, затем, одну из этих пластинок, держа ее горизонтально, он привел в колебание смычком, то нижняя пластинка дала совершенно те же звуковые фигуры, что и верхняя; таким образом колебания одной пластинки передавались другой через всю длину доски без изменения. После этого Савар усложнил этот опыт следующим образом. Он соединил разнообразным образом ряд пластинок неодинаковой длины из стекла и дерева, но так, чтобы в каждой паре звенья были перпендикулярны друг другу. Когда любая из этих пластинок приводилась смычком в поперечное колебание, то непосредственно связанная с нею пластинка приходила в продольное колебание, и последнее передавалось без изменения направления и даже скорости всем остальным пластинкам. Получив аналогичные результаты на ряде других видоизмененных опытов, Савар счел возможным вывести как общий закон следующее заключение: колебания передаются от одного тела к другому всегда таким образом, что они сохраняют направление, параллельное прежнему; поэтому все виды колебаний — поперечное, продольное и вращательное — следует рассматривать, как частные случаи единого общего для всех тел вида движения, производимого молекулярными колебаниями, которые видоизменяются соответственно направлению действующей силы. Братья Вебер согласились с тем, что резонанс может вызывать в телах колебания во всевозможных направлениях; при этом отметили, что в самостоятельно и свободно звучащих телах все-таки встречаются только три, охарактеризованные Хладни формы колебания. Они, со своей стороны, считали необходимым (и для стоячих колебаний, принимая во внимание первоначальное направление волн) различать двоякого рода колебания: первичные, где колебания (производимые утолщением и утоньшением тела) по своему направлению совладают с направлением распространения волны, и вторичные, где колебания (вызванные боковыми изгибами) совершаются перпендикулярно к этому направлению.
Вторичные колебания натянутого каната были полностью и успешно изучены Эйлером. Они еще более всего похожи на водяные волны. Здесь каждому стоячему колебанию предшествует поступательное, которое мало-помалу успокаивается, но никогда вполне не уничтожается, так что стоячее колебание всегда связано с некоторым волнообразным движением. Общеизвестный факт, что характер звука струны зависит от места, где на нее действует удар, определяется, конечно, как различием всей фигуры колеблющейся струны, так и одновременно существующими остатками поступательных колебаний. Подобное же явление повторяется на металлических прутьях, стеклянных палочках и стеклянных трубках, приведенных во вторичные колебания; и здесь, без сомнения, возникают волны, которые, встречаясь через правильные промежутки, производят стоячее колебание; но только скорость распространения волн здесь другая, гораздо большая, чем в струне.
Рассматривая поступательные первичные колебания воздуха, братья Вебер нашли замечательное явление, что поступательная волна может оставлять позади себя воздух в покое, что, например, стук в какой-либо точке воздуха бывает слышен лишь в течение короткого мгновения, но никак не все время, пока волна переходит далее от слоя к слою. Они объясняют это явление следующим образом. Если вообразить себе по середине трубки две частицы воздуха более плотными, чем все остальные, то это уплотнение будет выравниваться в обе стороны; если же все частицы одинаково плотны, но две средние частицы сторону, одновременно действуют оба условия, то вперед будет распространяться уплотнение, а назад разрежение; если же, как это и бывает при сотрясении воздуха, направленном в одну сторону одновременно действуют оба условия, то вперед будет распространяться удвоенное уплотнение, а в обратном направлении уплотнение и разрежение будут уравнивать друг друга и создадут состояние покоя.
Звучащий воздух в органной трубе, как и во всяком другом духовом инструменте, а также и в человеческом голосовом аппарате, находится в стоячем первичном колебании. Процесс, посредством которого он приводится в стоячие колебания, тот же, как в воде и как при вторичных колебаниях струн. Именно, в органной трубе колебания воздуха отражаются не только при закрытом, но и при открытом верхнем конце, но только в первом случае волна сохраняет свой характер, а во втором она обращается, т. е. из сгущающей она превращается в разрежающую, и наоборот. Во флейтах воздух втекает через щель не равномерно, а попеременно сгущается и разрежается и таким образом приходит в состояние колебания. Периодические толчки воздуха при быстром втекании его через отверстие можно наблюдать при топке печей: если отверстие в печной дверце сделать достаточно узким, то воздух попеременно то втягивается, то задерживается, производя таким образом пульсацию. Братья Вебер полагают, что подобный процесс является причиной звучания трубки, внутри которой горит водородное пламя.
Г. Вебер полагает, что в язычковых трубах, язычок не является источником звучания тела, а лишь механическим средством для попеременного открывания и закрывания отверстия. Во всяком случае, его движения зависят не столько от присущей ему упругости, сколько от движения воздушных волн, пробегающих вперед и назад по длинной трубке: язычок не сам собою движется, а совершает вынужденные колебания. Впрочем, теория духовых инструментов все еще сильно нуждается в более полной разработке, особенно слабо она до сих пор была разработана с математической стороны. Лангранж откровенно признавался, что его формулы еще очень несовершенно объясняют связь наблюдаемых явлений с размерами духовых труб и положением их отверстий. Работы же Пуассона показали, что a priori нельзя правильно определить даже самого низкого основного тона духовой трубы.
Рассматривая в последнем отделе своего сочинения волны в их отношении к свету, братья Вебер указывают на необоснованность возражений против волновой теории, высказанных Ньютоном, а также позднее Био и Малюсом. «Что касается учения Ньютона о свете, — говорят они на стр. 574, — то вместе со всеми физиками и вместе с Био его следует, действительно, признать мастерской абстракцией из опыта, но теория истечения является чисто вспомогательным средством, придуманным для того, чтобы придать выведенным оптическим законам наглядность без малейшего, однако, притязания на то, чтобы это наглядное объяснение соответствовало действительной сущности света. С этой точки зрения теория истечения, конечно, полезна, хотя и не вполне достигает цели, оставляя без объяснения явления интерференции и дифракции. Если же необходима такая гипотеза о сущности света, которая привела бы учение о свете в согласие с другими естественными силами и их законами, и если вообще не считать поиски подобной гипотезы пока преждевременными, то, конечно, волновой теории света должно быть отдано решительное предпочтение перед теорией истечения».
Исследование братьев Вебер приятно поражает не только искусной постановкой опытов, но и ясностью взгляда на сущность процессов, равно как и наглядностью их изображения. Исследование Савара, будучи равнозначным этой работе в первом смысле, уступает ей в прочих отношениях. Новые взгляды Савара на колебания тел, вызываемые резонансом, побудили, его к дальнейшему исследованию звучащих тел, в которых колебание вызывается резонансом.
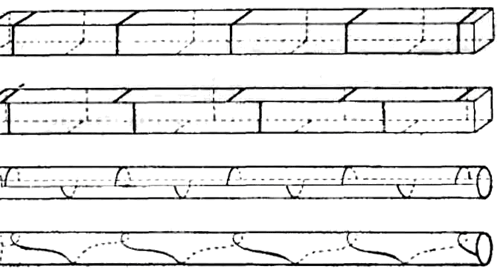
Опыты над узловыми линиями твердых тел, начатые им в 1820 г. и производившиеся в 1824 г., он закончил в 1837 г.2. Если посыпать поверхность продольно колеблющегося стержня тонким сухим песком, то получается известное число узловых линий, расположенных перпендикулярно к длине бруска, причем на одной стороне стержня эти линии располагаются так, что они оказываются по середине промежутков между узловыми линиями противоположной стороны. Число этих узловых линий тем больше, чем толще, при прочих равных условиях, стержень. На четырехугольных и цилиндрических стержнях узловые линии противоположных сторон могут соединяться в винтовые линии, как показывают приложенные рисунки. Так как зависимость узловых линий от размеров стержня та же, что и «при поперечных колебаниях, то Савар пришел к выводу, что узловые линии вызываются поперечными колебаниями, сопровождающими продольные, и объяснил это следующим образом (черт. 11). Когда продольно колеблющийся стержень сокращается по своей длине, образуются изгибы, как при поперечных колебаниях, но эти изгибы не могут перейти на противоположную сторону, так как следующее за сокращением растяжение уничтожает изгиб. Таким образом, изгиб происходит как половинное колебание. Взаимное расстояние узловых линий даже при одном и том же опыте не везде одинаково, что происходит вследствие неоднородности внутреннего строения тел. Если равномерный по своей структуре стержень немного согнуть, а затем перед опытом более или менее выправить, то узловые линии изменяются; для этого также достаточно сжать брусок посредине пальцами.
Поразительна величина силы, развиваемой продольными колебаниями, если ее сравнить с незначительностью тех усилий, которыми она вызывается. Так, например, если по стеклянной трубке в 2—3 м длины с поперечником в несколько миллиметров слабо провести мокрыми пальцами, она начинает быстро втягивать в себя лежащий в ней свинцовый шарик даже вопреки силе тяжести. Свободно подвешенный шарик отталкивается с большой силой концом колеблющегося стержня. Для того чтобы стеклянный стержень длиною в 0,968 м и толщиной в 29,10 мм получил удлинение, вызываемое в нем продольными колебаниями, нужно было бы приложить к нему силу не менее 900 кг; действительно, это удлинение составляет 0,210 мм. Поэтому стеклянные трубки и палочки в 2—3 м длины очень легко разламываются, когда колебания достигают известной величины.
Для наблюдения движения воздуха в звучащих трубах Савар употреблял натянутые на кольца и обсыпанные песком перепонки, которые подвешивались на тонкой нити, подобно чашкам весов, и опускались в полость труб. Этот прибор был усовершенствован Гопкинсом, который применил его для более точных опытов. Последний состоял из стеклянной трубки, в верхней части которой для увеличения и уменьшения длины перемещалась плотно пригнанная металлическая трубка; внутри трубки была установлена маленькая рамка, обтянутая тонкой перепонкой, которую можно было перемещать по желанию выше и ниже. Кроме того, изменяя натяжение, перепонку можно было настраивать на тон трубы, так что она слегка резонировала. Этим путем Гопкинс подтвердил вообще прежние данные касательно основных тонов и обертонов, как в открытых, так и в закрытых трубах, но, кроме того, установил, что движение в узловых точках вследствие неполного отражения волн не сводится к нулю, а только снижается до некоторого минимума, что в закрытых трубах расстояние первого узла от нижнего открытого отверстия не равно, а несколько больше 1/4 волны, а в открытых трубах расстояние первого узла от верхнего открытого конца заметно меньше 1/4 волны. Прежние акустики-математики не обращали внимания в своих исследованиях на передачу движения веществу, находящемуся у конца трубы, и потому помещали узлы прямо в конце трубы. Это и было причиной неполного согласия их результатов с опытом, и в то же время этим объясняется, почему они не могли вывести из своих формул внезапного прекращения звучания с прекращением действия внешней возбуждающей причины. Гопкинс объясняет это ослабление звука отражением, указывая, что после 5—6 отражений сила звука падает до незаметной величины.
По примеру Савара Гопкинс вызывает колебания воздуха в трубах не вдуванием его, которое помешало бы наблюдению с перепонками, а при помощи поставленной под трубой стеклянной пластинки, которая приводилась в колебание смычком. При этом оказалось, что когда труба покрывала различно колеблющиеся части пластинки, получались несомненные признаки интерференции звука. Мы уже упоминали, что Юнг охарактеризовал толчки, наблюдаемые при созвучии тонов, как явление интерференции. В. Вебер наблюдал в 1826 г. неодинаковость силы звука колеблющегося камертона или даже прута по различным направлениям и объяснил это явление тоже интерфенцией волн, исходящих от противолежащих сторон прута. Гопкинс добился полного уничтожения колебаний, прямого погашения одного тона другим при помощи вилообразной трубки ![]() , оба колена которой он поставил против противоположно колеблющихся частей звучащей пластинки: при этих условиях перепонка, натянутая на верхнем конце трубки, оставалась в покое. Впрочем, уже несколько ранее Роберт Кен достиг той же цели, пропуская тон через трубку с ответвлением
, оба колена которой он поставил против противоположно колеблющихся частей звучащей пластинки: при этих условиях перепонка, натянутая на верхнем конце трубки, оставалась в покое. Впрочем, уже несколько ранее Роберт Кен достиг той же цели, пропуская тон через трубку с ответвлением ![]() , расходящиеся ветки которой отличались друг от друга по своей длине на 1/2 волны.
, расходящиеся ветки которой отличались друг от друга по своей длине на 1/2 волны.
Распространение звука в жидкостях, т. е. существование колебаний (первичных), заключающихся в уплотнениях в разрежениях, долгое время отрицалось, так как жидкости тогда казались несжимаемыми. Поэтому, когда на опытах со слухом людей и животных был доказан факт прохождения звука через воду, возможность его объясняли упругостью заключенного в воде воздуха. Правда, Нолле удались аналогичные опыты и с водою, совершенно освобожденной от воздуха; а с другой стороны Франклин, на основании прямых опытов, утверждал, что звук в воде распространяется гораздо быстрее, чем в воздухе; но эти факты находились в прямом противоречии с тогдашними данными о сжимаемости и упругости воды. Лишь после того, как сжимаемость и упругость жидкостей были установлены, явилась возможность свободнее исследовать и вопрос о звукопроводности воды. Савар путем наблюдений над пластинками, плавающими на воде и посыпанными песком, установил в 1826 г., что характер прохождения звука в жидкостях тот же, что и в твердых телах. При этом оказалось, что вибрации звучащего тела передаются пластинкам первичными колебаниями из воды как снизу вверх, так и в горизонтальном направлении, т. е. во всевозможных направлениях. Точное определение скорости распространения звука в воде было произведено в следующем году Колладоном и Штурмом. Последние спустили на одной станции в воду колокол и затем вызывали звук ударами молотка по этому колоколу, а на другой станции для восприятия звука погрузили в воду нижней частью слуховую трубку, расширенное отверстие которой было затянуто перепонкой; верхняя же суженная часть этой трубки выдавалась над водой, и к ней прикладывалось ухо наблюдателя. Без этой трубы звуки в воздухе на второй станции совершенно не были слышны. Опыты эти производились на Женевском озере между Тононом и Роллем, где озеро, при ширине в 14 000 м и глубине в 140 м, имеет почти плоское дно. Температуры на обеих станциях были соответственно 7,9 и 8,2°; расстояние между ними — 13 487 м. При 40 наблюдениях время распространения звука определялось в 9,25—9,5 сек.; следовательно, скорость распространения оказалась равной 1435 м в секунду. Теоретическое исчисление этой скорости по наблюденной сжимаемости воды, без принятия в расчет тепловой постоянной Лапласа, дало 1528 м; отсюда следует, что для жидкостей эту постоянную можно считать очень близкой к единице.
После того как звукопроводность жидкостей была доказана, попытались привести самые жидкости в звуковые колебания. С этой целью Каньяр-Латур 1 продувал трубки под водою с помощью каучукового мешка, либо приводил в движение сирену, пропуская через нее струю воды, либо, наконец, натирал мокрой тряпкой стеклянные наполненные водою трубки (запаянные снизу или загнутые сифоном). Трубка в 1 м длины с запаянным нижним концом дала, таким образом, 385 кол/сек, другая, изогнутая сифоном, — 775 кол/сек. Вычисленная отсюда скорость распространения звука в воде дала отклонение от полученного непосредственным путем числа Колладона и Штурма; подобные отклонения продолжают наблюдаться до последнего времени.
Еще большее значение и вполне заслуженную известность имеют опыты Савара о пределах слышимости, так как они впервые производились при помощи прибора, дающего возможность непосредственно определять число колебаний какого-нибудь тона. До этого времени прямой подсчет числа колебаний был невозможен, и число колебаний исчислялось лишь косвенным путем. Колесо Станкари едва ли применялось кем-либо другим кроме самого изобретателя, да и он, по-видимому, не получил с ним точных результатов. Первый механический счетчик звуковых колебаний был устроен в 1819 г. Каньяр-Латуром 2, который дал своему прибору очень мягкое название сирены. Последняя в основном состояла из легкого вращающегося около оси металлического диска, по окружности которого были вырезаны прямоугольные зубцы равной ширины с равными между ними промежутками, или в котором, несколько отступя от окружности, были вырезаны отверстия равной величины на равных расстояниях друг от друга. Из отверстия тонкой трубки можно было пускать струю воздуха или какой-нибудь жидкости на зубцы или в промежутки между ними; при вращении диска струя, периодически прерываясь, давала определенный тон. Вскоре после того зубцы на окружности или отверстия в диске стали прорезывать косо, так что диск приводился в движение самим током жидкости. К аппарату мог быть присоединен особый счетчик, который давал возможность определить число оборотов колеса, а следовательно, и частоту колебаний. Впоследствии Зеебек в своих теоретических исследованиях часто прибегал к сирене и рекомендовал ее для общего пользования. Он постарался усовершенствовать этот прибор; с этой целью он расположил отверстия несколькими концентрическими кругами, дабы иметь возможность сравнивать аккорды тонов. При определении высшего предела слышимости Савар тоже воспользовался сиреной, но для получения более отчетливых тонов он вместо воздушного тока применял какое-либо маленькое клинообразной формы тело, например игральную карту, о которую и ударялись зубцы. Таким образом, верхний предел слышимости он установил при 24 000 полных или 48 000 простых колебаний в секунду. Но так как уже при 15 000 колебаний тоны были слабо слышны, а потом они были едва ощутимы, то этим путем нельзя было точно установить порог слышимости. Во всяком случае, предел слышимости зависит от способа воспроизведения звуков. Для определения предела слышимости низких тонов он устроил другой аппарат, состоявший из железной полосы в 21/2 фута длины, 2 дюйма ширины и 6 дюймов толщины, вращающейся около оси, которая проходила через широкие стороны полосы. При своем вращении полоса проходила свободным концом между двумя тонкими пластинками не более, как на расстоянии 1 мм от каждой. При этом получался настолько сильный тон, что он заглушал и человеческий голос и органную трубу. По оценке лиц, в большом числе присутствовавших при этих опытах, при 14—16 простых колебаниях в секунду был еще слышен протяжный тон. Однако и этот предел Савар не считает абсолютным, потому что случалось улавливать и более низкие тоны, когда полоса замедляла свою скорость. Заключение Савара о движениях в слуховом органе также очень важно. Он нашел, что слабо натянутая перепонка приводится в колебание любыми звуками и что воздушные колебания приводят ее в движение совершенно так же, как твердое тело, поставленное перпендикулярно к ее плоскости. Этим опровергалось ходячее в то время мнение, будто барабанная перепонка должна изменять собственный тон для восприятия различных звуков, и устанавливалось значение слуховых косточек для передачи колебаний.
К этим исследованиям, которые, соприкасаясь более или менее с вопросом о молекулярных движениях или, по крайней мере, об изменении 'молекулярного состояния в телах, представляли собою известные этапы на пути к развитию молекулярной физики, присоединилось еще одно новое открытие, от которого с указанной точки зрения ожидали очень многого. В январе 1805 г. в Геттштедте Шварц сделал случайное наблюдение, что только что застывшая пластинка, будучи положена на наковальню, издает тон. По поводу этого открытия Гильберт съездил в Геттштедт, где заметил, что это звучание сопровождается дрожанием металлической массы, и описал настоящее явление в своих Анналах. Но так как он полагал, что имеющихся наблюдений еще недостаточно для объяснения этого факта, то оставалось только ждать новых опытов. В 1829 г. А. Тревельян, собираясь смолить варом при помощи горячего куска железа, прислонил слишком сильно накаленное железо к куску свинца и заметил то же явление, что и Шварц. Причину колебаний он приписал расширению холодного металла в непрерывно чередующихся местах соприкосновения; путем многочисленных опытов определил, какие металлы наиболее пригодны для того, чтобы служить подставкой, и какие — в качестве качающегося тела, и нашел наиболее целесообразную форму для подставки. Фарадей, докладывая 1 апреля 1831 г. Королевскому обществу об этом явлении, присоединился к воззрениям Тревельяна и объяснил преимущество свинца, в качестве холодного металла, значительным его тепловым расширением при наличии в то же время слабой теплопроводности. Форбс, бывший на докладе Фарадея, сделал 18 марта и 1 апреля 1833 г. сообщение на ту же тему Королевскому обществу в Эдинбурге. Он предположил, что при переходе тепла из тела с большой теплопроводностью в тело с меньшей теплопроводностью происходит отталкивание, род отдачи (как при вытекании всякой жидкости), и на основании своих опытов пришел к следующим законам: 1) между однородными веществами колебания никакого не происходит; 2) оба вещества должны быть металлические; 3) колебания происходят с силой, пропорциональной разности теплопроводности, причем более дурной проводник должен быть холодным металлом. Однако Зеебек пришел к иным результатам. Любой горячий металл на любом холодном (из того же или из другого вещества) может давать колебания, лишь бы форма металлов была такова, чтобы теплота в холодном распространялась в стороны значительно меньше, чем холод в горячем. Тиндаль 6 опроверг все три закона Форбса. Он получал тоны от железа на железе, от меди на меди, от олова на олове, от латуни на горном хрустале, дымчатом топазе, плавиковом шпате и особенно резко на каменной соли, которая оказалась для этих опытов наиболее подходящей. Что касается объяснения данного явления, Тиндаль и другие физики остались при первоначальном мнении Тревельяна-Фарадея. К этому же периоду относится окончательное выяснение сущности комбинационных тонов. В. Вебер уже в 1828 г. высказал мнение, что комбинационные тоны двух одновременно звучащих простых тонов можно найти, развернув частное из числа колебаний обоих тонов в дробь и определив ее приближения. Однако он сам при этом отметил большое расхождение между вычисленными и наблюденными величинами. Гелльстром дал более простое, но и более верное правило: первый комбинационный тон определяется разностью числа колебаний составных тонов, а все остальные комбинационные тоны высшего порядка получаются из созвучия простых тонов с комбинационными тонами низшего порядка. Шайблер пришел принципиально к тому же результату и воспользовался им для установления чистых тонов посредством ряда камертонов, с числами колебаний, отличающимися друг от друга та четыре единицы.