Аналитическая механика с Лагранжем принципиально достигла своей законченности. Единая формула охватывала все проблемы статики, а из другой, тесно с нею связанной, вытекало и решение всех проблем динамики.
В лице Лагранжа наиболее наглядно выявилась мощь анализа, позволяющего получать строго логически решения всевозможных частных проблем с помощью единого, совершенно общего метода рассуждения. Но с другой стороны, в нем выявились, в особенности для независимых умов, и недостатки его чисто аналитического метода, сказывавшиеся в частом несоответствии его приемов решения с приемами, связанными со специальными свойствами отдельных задач, следствием чего зачастую являлась ненаглядность, отсутствие непосредственной очевидности и, наконец, трудность правильного специализирования общих формул.
Для применения своего принципа виртуальных скоростей к решению частных случаев равновесия, Лагранж был вынужден очень сложным путем вывести из него шесть известных условий и указать их геометрическое значение. Пуансо, в своих «Elements de statique» (Paris 1804) («Начала статики») вернулся к синтетическому методу и те же шесть уравнений вывел геометрически из возможности различных видов движения тела (черт. 9).
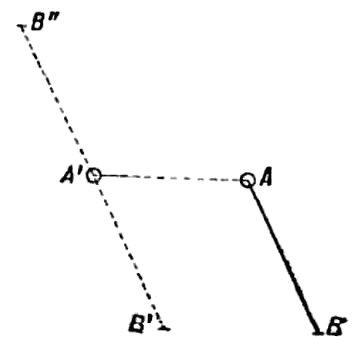
Когда все действующие силы приложены к одной точке или, по крайней мере, сходятся по своему направлению в одну точку, то их можно легко сложить геометрически по правилу параллелограмма сил и таким образом графически определить совокупное их действие. Но если этого условия налицо нет, следует перед сложением перенести силы в одну точку, что, однако, без введения новых сил невыполнимо. Так, если силу, пропорциональную отрезку АВ и одинаково с ним направленную, желают переместить в точку А' того же тела, то это можно сделать не иначе, как допустив в точке А' существование двух равных, параллельных, но противоположно направленных сил. Тогда помимо силы А'В', которую можно рассматривать как перемещенную силу АВ, получается система сил АВ и A'B". Эти равные, параллельные и противоположно направленные силы не имеют результирующей, не могут быть заменены одной силой и производят, следовательно, не перемещение, а вращение тела. Пуансо назвал эту систему парою сил. Здесь момент вращения пропорционален произведению величины действующих сил на их расстояние. Простыми построениями можно показать, что пару сил можно произвольно перемещать и вращать в ее плоскости или даже в плоскостях ей параллельных, откуда следует, что действие пары зависит только от момента пары и направления ее плоскости. Если представить себе перпендикуляр, восстановленный к этой плоскости, и отложить на нем длину, пропорциональную величине момента, то величиной этого отрезка и его направлением пара сил вполне определяется. Пуансо называет этот отрезок осью пары сил. Таким образом, сложение пар сил в параллельных плоскостях сводится к сложению отрезков прямой линии. Далее, с помощью опять-таки простых построений доказывается, что пары, расположенные в непараллельных плоскостях, тоже складываются в единую результирующую пару, ось которой получается из осей слагаемых пар по закону параллелограмма сил.
Итак, какие бы силы ни действовали на тело, их действие всегда можно свести к одной силе и одной паре сил: следовательно, условия равновесия сводятся к тому, чтобы результирующая сила и результирующая пара были равны нулю, или, говоря геометрически, к невозможности перемещения и вращения тела. Если, кроме того, результирующую силу отнести к трем осям координат, а результирующую пару к трем координатным плоскостям, и каждую из шести проекций приравнять нулю, то получаются те старые шесть условий равновесия аналитической механики, которые обозначают отсутствие перемещений по какому-либо из трех взаимно перпендикулярных направлений и отсутствие вращений около какой-либо оси, параллельной последним. Ко второму изданию своей статики Пуансо прибавил особую статью «Mémoire sur la composition des moments et des aires» («О сложности моментов и площадей»), имевшую своей целью частью еще более выяснить теорию пар, частью указать общие крайне интересные положения, касающиеся величины результирующих пар, частью, наконец, разъяснить применение пар сил к решению вопросов динамики. Объем и ценность своего нового механического метода Пуансо сам вполне правильно определяет в предисловии ко второму изданию «Статики»: «При этом можно будет убедиться, что пара сил имеет значение не какого-либо единичного случая, а существенного элемента механики, которого в ней до сих пор недоставало... Кроме того, легко заметить, что в динамике сложению пар сил соответствует сложение вращательных движений... вследствие чего — при невозможности для нас представить себе наглядно движение тел иначе, как в виде одновременного перемещения и вращения около какой-либо точки — параллелограмм анализа движения всякого тела конечной величины, и притом началами анализа движения всякого тела конечной величины, и притом началами, непосредственно вытекающими из самой природы вещей. Наконец, можно будет заметить, насколько метод пар сил легок и насколько он превосходит прежний метод, если принять во внимание, во-первых, что из него тотчас же вытекают все условия равновесия, теорема Эйлера об отнесенных к отдельным осям суммах моментов какой-либо системы сил, наибольший момент и неизменная площадь поверхностей Лапласа; во-вторых, что настоящий метод дает возможность дополнить эти части механики новыми теоремами, касающимися центральной оси моментом (как мы ее назвали) и единственной площади минимальной поверхности между бесконечным числом максимальных поверхностей».
Вопрос о наглядном рассмотрении движения теле, о возможном переводе его из одного определенного положения в другое, намеченное Пуансо в только что приведенном предисловии, он развивает в новой фундаментальной работе «Théorie nouvelle de la rotation des corps» (Paris 1834) («Новая теория вращения тел»). Здесь рассматриваются, главным образом, сложение и разложение вращений, а также вращение тела около одной неподвижной точки. Для последнего случая он предварительно обосновывает характерное положение, согласно которому всякое вращение тела около неподвижной точки может быть осуществлено качением неподвижно связанного с телом конуса по другому неподвижному конусу, вершина которого остается в постоянном соприкосновении с вершиною первого конуса.
Эта чисто геометрическая теория движения, не принимавшая в расчет ни времени, ни силы, была позднее дальше разработана Родригом, Шалем, Мебиусом и ныне представлена в любом учебнике механики. Но в начале идеи Пуансо прививались очень туго, кажущееся всемогущество анализа задерживало распространение синтеза. Пуассон и Навье в своих учебниках механики тридцатых годов впервые упоминают о парах сил и методах Пуансо. В Германии на них усиленно обращают внимание Мебиус (Lehrbuch des Statik, 1837) и Фердинанд Миндинг (Handbuch der theoretischen Mechanik, 1838), и примерно в тот же период синтетический метод начинает снова приобретать значение и в геометрии.
Аналитическая механика развивалась в это время, конечно, в общем по путям, проложенным Лангранжем, претерпевая, правда, некоторые изменения и более или менее прогрессируя. Такой крупный ученый, как Гаусс попытался установить новый принцип механики, который должен был обнять непосредственно и в самом общем виде все статистические и динамические проблемы механики. Принцип этот гласит: «Движение системы материальных точек, связанных между собою каким-либо образом и подчиненных в своих перемещениях каким-либо внешним ограничениям, совершается в каждое мгновение в наибольшем возможном соответствии со свободным движением или с наименьшим возможным ограничением. Гаусс считает это начало непосредственно очевидным, и потому предпочитает его началу виртуальных скоростей. Однако первое справедливо лишь условно, поэтому и вывод нельзя считать бесспорным. В словесной формулировке за этим положением можно еще признать очевидность, но последняя исчезает при переводе его на математический язык. Ранее чем применить данное начало, следует предварительно математически определить понятие «ограничение», а когда соответствующее выражение для него найдено, следует еще доказать, что оно при всех возможных обстоятельствах будет представлять наименьшую величину. А так как применение принципа наименьшего ограничения Гаусса не создает никаких преимуществ по сравнению с началом виртуальных скоростей, то хотя он и был принят с уважением, но действительного успеха не имел.
Плодотворнее оказалось установление Гамильтоном нового или, скорее, видоизменение и расширение старого механического принципа. Началу наименьшего действия Мопертюи, которое он назвал принципом стационарного действия, Гамильтон противопоставил более широкий принцип, названный им началом варьирующего действия. Первое начало гласит: При всяком несвязанном движении системы из одного определенного начального положения в другое определенное положение действие необходимо стационарно (т. е. вариация его равна нулю), если внутренние силы системы консервированы (т. е. если они по своей природе таковы, что в равные времена они производят равную работу). Начало же варьирующего действия определяет его вариацию, когда начальные и конечные положения свободного движения, равно как и работа сил, изменчивы. Кроме того, слово «действие», как это было уже замечено со времен Мопертюи, страдало неопределенностью, поэтому наиболее важным и решающим оказалось то обстоятельство, что Гамильтон придал ему определенный смысл и математическое выражение. Определив действие, как функцию суммы сил напряжения и живых сил системы, он не только показал, что начало наименьшего действия, принцип д'Аламбера и уравнения движений Лагранжа, при всем их внешнем формальном различии, по существу тождественны, но и доказал, что данное им начало представляет наибольшие удобства для самого общего применения.
По Кирхгофу особое удобство гамильтоновского начала заключается в том, что оно дает возможность сравнительно легко вводить в дифференциальные уравнения движения системы материальных точек вместо прямоугольных координат другие переменные. Гельмгольц утверждает, что начало наименьшего действия (в форме, данной ему Гамильтоном) представляет, по всей вероятности, самый общий закон для всех вообще естественных (по крайней мере, для всех обратимых) процессов. «Отсюда уже теперь становится ясно, — говорит он, — что сфера применения начала наименьшего действия выходит далеко за пределы механики весомых тел и что казавшиеся преувеличенными надежды Мопертюи на признание за его законом абсолютной всеобщности, по-видимому, начинают сбываться, несмотря на скудность механических доказательств и противоречивость метафизических умозрений, которые автор положил в свое время в основание своего нового начала».
Работы Гамильтона тесно соприкасались с развитием механики и математической физики еще и с другой стороны. Точное и удобное определение понятия действия, благодаря которому начало наименьшего действия собственно и получило широкое применение, было достигнуто Гамильтоном тем, что он ввел в рассмотрение новые функции и, главным образом, функцию, которую он назвал силовой функцией (force function). Это нововведение было собственно физикой использовано в большей мере, чем самое начало Гамильтона. В этом деле Гамильтон, будучи самостоятельным, не был, однако, первым. Уже за шесть лет до него, а именно в 1828 г., Грин в очень общем виде применил ту же функцию для определения физических сил и тоже дал ей особое название потенциальной функции. Но работы Грина, а по началу и работы Гамильтона, не обратили на себя должного внимания, и только в 1840 г. они получили всеобщую известность и признание благодаря Гауссу, который эту функцию назвал короче потенциалом. Впрочем, применение этой функции для определения притяжений, действующих по закону тяготения, следует отнести еще к 1777 г., когда Лагранж доказал, что производные этой функции но определенным координатам равны составляющим силы, разложенной по этим координатам. Вскоре затем Лаплас дал знаменитое дифференциальное уравнение функции v:

применимость которого Пуассон, однако, должен был ограничить точками, лежащими вне действующих масс. Пуассон показал, что в общем виде, без этого ограничения, уравнение имеет следующий вид:

где k обозначает плотность массы в соответственной точке; следовательно, пользуясь этим уравнением, можно при посредстве потенциала определить плотность массы в любой точке.
Математики определили потенциал как функцию, производные которой по координатам равны составляющим действующей силы по осям координат. При этом под действующей силой подразумевали только тяготение, и потенциал применялся только для решения проблем притяжения. Однако благодаря почину Грина потенциал стал приобретать все большее значение и в теории магнетизма и электричества; при его помощи Грин разрешил чисто математическим путем много задач об электрическом и магнитном влиянии, а равно о распределении магнетизма и электричества на телах. А так как благодаря этому потенциал по своему значению вышел далеко за пределы чистой математики, то в последнее время понятие о потенциале совершенно освободили от его прежнего аналитико-математического определения; в настоящее время его определяют по его отношению к механической работе, благодаря чему для новейшей физики открылась возможность обходиться без ставшего несколько сомнительным понятия силы. Соответственно сказанному, например, электрический потенциал в данной точке электрического поля измеряется работой, производимой электрическими силами, когда единица электричества, сообщенная этой точке без каких-либо нарушений в состоянии электрического поля, удаляется отсюда на бесконечно далекое расстояние или до точки, где потенциал равен нулю.
К этому же времени относится и точное установление понятия работы, и введение его в теоретическую механику. Произведение силы на пройденный ею путь применялось уже в XVIII веке при отдельных механических исследованиях. Карно (отец) обозначил его в 1876 г. термином moment d'activite, а Монж — effet dynamique. И только Понселе впервые в 1826 г. ввел в обиход термин работа (travail). Правда, слово работа встречалось и прежде; так, Юнг уже в 1807 г. утверждал, что работа пропорциональна живой силе. В своих «Lectures on natural philosophy» (London 1808, 1, стр. 78—79) он говорит: «Почти во всех случаях, встречающихся в практической механике, работа, необходимая для воспроизведения движения, пропорциональна не моменту, а энергии произведенного работой движения». «Словом энергия следует обозначать произведение массы или веса тела на квадрат числа, выражающего скорость». Этою эквивалентностью между работой и живой силой (или энергией) и воспользовался Понселе как наилучшим средством для разрешения механико-технических задач, положив в основу своего знаменитого сочинения «Introduction a la mécanique industrielle» (Metz 1829, 2-е изд., 1841) в качестве главного положения общий принцип передачи механической работы.
Относительно всеобщности этого начала он высказывается (Introduction a la mécanique industrielle, стр. X—XI) в очень характерных выражениях: «В самом деле, начало виртуальных скоростей в применении его к действительным движениям тел — если при этом принимать во внимание все внутренние и внешние силы, которые увеличивают или уменьшают движение — приводит посредством простого элементарного суммирования полученных количеств работы к принципу передачи работы, к равенству суммы живых сил (mv2) и удвоенной алгебраической суммы всех работ, исходя из такой точки зрения этот принцип обнимает собою все законы взаимодействия сил и притом в такой форме, которая значительно облегчает применение его к технической механике, т. е. к той части механики, которую прямо можно было бы назвать наукой о работе сил». В конце теоретической части своего сочинения Понселе снова возвращается к вопросу о передаче работы и показывает (стр. 131), что работа или живая сила никогда не получается из ничего и никогда не уничтожается, что в основании происхождения работы или живой силы всегда лежит какое-нибудь преобразование этих самых агентов.
При всем том не следует, однако забывать, что мы здесь находимся пока еще исключительно в чисто механической области и что понятия энергия, работа и потенциал здесь интерпретируются только механически. Полное значение для всей физики эти понятия получили лишь после того, как совершился великий переворот в наших воззрениях на природу и действие сил, после того, как был установлен закон сохранения силы. Было бы очень интересно и поучительно более внимательно исследовать то обоюдное влияние, которое оказали друг на друга приведенные выше понятия и идея сохранения сил. Первые, возникнув почти незаметно, распространяются постепенно и в некоторых кругах приобретают все большее значение, но до общего их признания дело не доходит. И вдруг, как будто без предварительной подготовки, появляется закон сохранения силы, и тогда только эти понятия оказываются настолько мощными, что они преобразуют самую идею силы или даже совсем вытесняют ее. Таким образом, с первого взгляда создается впечатление, будто приведенные понятия были оплодотворены идеей сохранения силы; но более глубокое исследование могло бы, быть может, показать и обратное, а именно — постепенное возникновение закона сохранения силы из указанных предшествовавших ему по времени понятий.
Хотя новые понятия прилагались преимущественно к внешнему взаимодействию тел, однако, математическая физика не упускала из виду исследования и внутренних изменений в телах. Исследования о двояком преломлении и поляризации света в различных веществах, с основанной для их объяснения Френелем теорией упругости тел, побудили наиболее выдающихся математиков к дальнейшим работам в этой области. Здесь, наряду с многократно упоминавшимся Пуассоном, следует на первом месте поставить Коши, который попытался подчинить математическому анализу все отделы физики, за исключением только электричества и магнетизма. К сожалению, его работы, имеющие огромную ценность с математической стороны, не имеют равной ценности для физики. С одной стороны, гипотезы о строении материи, которые он по необходимости должен был положить в основу своих математических исчислений, не обладают очевидностью; с другой стороны, выводимые им отсюда результаты не всегда настолько хорошо совпадают с опытными данными, чтобы в них, обратно, можно было найти подтверждение этих гипотез. Больше того, как раз работы Коши и — в меньшей степени — Пуассона были некоторыми учеными использованы для того, чтобы показать, что математическая дедукция, подобно философской, сама по себе не в состоянии приводить к правильному познанию законов природы без постоянного содействия опыта.
Как уже было отмечено, исследования Пуассона и Коши касались своею механическою стороною преимущественно теории упругости и распространения движений в упругих средах. При этом оба пришли к интересным выводам о природе материи, казавшимся крайне важными для господствовавшей тогда атомной теории. Лаплас заметил по поводу их выводов, что математики при своем интегрировании принимали материю сплошной и таким образом вступали в принципиальное противоречие с атомистикой, но что вытекающая отсюда погрешность, вследствие перевеса заполненного материей пространства над пустым, во всяком случае, исчезающе мала. Впоследствии Пуассон (преимущественно благодаря своим работам по волновой теории света) пришел к убеждению, что допущение сплошного заполнения пространства в целях интегрирования возможно исключительно лишь для тех случаев, когда имеются в виду только действия во вне, и что в других случаях следует вместо интегралов применять суммы конечных разностей, т. е. считать материю не сплошной, а состоящей из отдельных частей. Его примеру последовал и Коши, разрабатывавший в самом общем виде механику системы материальных точек или молекул, произвольно распределенных в пространстве и связанных силами взаимного притяжения и отталкивания. При этом опять-таки, в целях возможной общности, он силы принял равными произведению действующих масс на некоторую (неопределенную) функцию их расстояний. Когда упругость в системе масс была принята различной в разных направлениях, то в формулах оказалось множество постоянных; для систем с тремя взаимно перпендикулярными осями упругости число постоянных свелось к шести, которые могли быть определены путем наблюдения скорости распространения звука по соответственным направлениям. Как Коши, так и Пуассон применили свои формулы к выводу деформации однородных упругих тел под влиянием определенных натяжении или давлений, к определению колебании прутьев, пластинок, перепонок, струи и т. д. и, наконец, по крайней мере, первый из них — к разработке волновой теории света, к чему мы еще вернемся. Кроме того, оба они пытались проверить свои, полученные теоретическим путем результаты прямыми измерениями и здесь Коши оказался менее счастливым, чем Пуассон, который вообще давал гораздо больше числовых определений. Одно из таких определений долгое время интересовало и физиков-экспериментаторов. Пуассон вывел из своих формул, что удлинение струны или проволоки, вызванное ее растяжением, вчетверо превосходит укорочение диаметра, перпендикулярного к направлению растяжения. Опыты Каньяра де-Латура подтвердили этот результат; однако более поздние измерения Вертгейма вместо 4 дали число 3, вследствие чего стало вероятным, что вообще это отношение для различных веществ различно. Чтобы закончить изложение главнейших успехов теоретической механики того времени, следует еще упомянуть о замечательных исследованиях Якоби 5 по вопросу о фигурах равновесия вращающихся несжимаемых жидкостей. Со времен «Treatise of Fluxions» («Учение о бесконечно малых») Маклорена существовало убеждение, что свободно вращающаяся в пространстве несжимаемая жидкость должна под влиянием центробежных сил принимать форму эллипсоида вращения. Как сообщает Якоби, в связи с утверждением Понтекулана, что фигурами равновесия могут быть только тела вращения, он принялся за исследование этого вопроса «из духа противоречия», которому он «обя-зан большинством своих открытий». И действительно, эта работа привела его к удивительному результату, что вращающаяся около оси жидкость, при известном отношении между квадратом угловой скорости, плотностью и силой взаимного притяжения частиц жидкостей, может отклониться от эллипсоида вращения и принять форму трехосного эллипсоида. Этот результат пролил совершенно неожиданный свет на возможную фигуру Земли и небесных тел.
К описанным исследованиям удобно будет присоединить попытки дальнейшей разработки теории волосности, хотя они и не носят в той же мере математического характера, как вышеописанные работы, оставаясь в более тесной связи с наблюдением и опытом. Гаусс удержал при объяснении этих явлений постулаты Лапласа и только постарался обосновать выводы законов волосности более строгим образом. Пуассон, наоборот, ввел в теорию новый момент — изменение плотности и напряжения жидкостей на поверхности. Граф Румфорд, наблюдая плавание иголок на воде, вывел отсюда заключение, что на поверхности воды образуется как бы жидкая пленка. Тогда Пуассон показал, что всякая теория, не принимающая во внимание изменения плотности на поверхности жидкости, недостаточна для объяснения явлении волосности. Каждая точка внутри жидкости, удаленная от ее границ более чем на радиус действия частиц, подвергается одинаковому воздействию со всех сторон, тогда как точка, расстояние которой от свободной поверхности меньше указанной величины, подвержена с разных сторон воздействию неодинаковых сил, вследствие чего плотность жидкости в пределах указанной сферы молекулярного действия является величиной переменной и отличается от плотности ее вне сферы. Aparo (Werke II, стр. 520) высказывает сожаление по поводу отношения Пуассона к теории Лапласа. «Возникает вопрос,— говорит он, — каким образом мог Лаплас выразить явления волосного притяжения в числах, если он в своих исчислениях упустил из виду истинную и единственную причину этих явлений. Я должен признать, что это представляет собою большой математический скандал, за распутывание которого следовало бы поскорее приняться лицам, у которых для этого имеется достаточно времени и таланта, чтобы вынести решение по поводу расхождения между такими большими умами, как Лаплас и Пуассон. Здесь речь идет о чести науки». Однако в большинстве учебников опытной физики теория Пуассона рассматривалась отнюдь не как противоположность лапласовской, а только как поправка к последней, согласно которой явления волосности должны выводиться из действия стенок трубки не на одни только прилегающие поверхности жидкости, но и на несколько более далекие слои ее. Следует отметить, что после Пуассона и математическая теория оказалась не в состоянии справиться со всеми трудностями этой проблемы — вследствие отсутствия точных данных о природе молекулярных сил, видоизменяющих плотность поверхностных слоев. Кирхгоф в своих лекциях по механике заключает главу о волосности следующим образом: «У жидкости, на которую действуют капиллярные силы, давление внутри изменяется так, как будто бы этих сил вовсе не было, но на бесконечно близком расстоянии от поверхности оно изменяется бесконечно быстро. Именно, капиллярные силы, действующие на частицы, лежащие на конечных расстояниях от поверхности, взаимно уничтожаются, на поверхности же они дают бесконечно большие результирующие. Если попытаться применить это понятие, то при исследовании капиллярных явлений возникают большие трудности; мы избежали их тем, что пошли иным путем, которым впервые воспользовался Гаусс». Однако связь между капиллярными явлениями и молекулярными силами, столь затруднявшая математическую разработку первых, вызвала после долгого застоя новые опытные исследования, которые давали поводы надеяться, что наши знания об этих силах расширятся. Линк опубликовал многочисленные опыты над высотой поднятия воды, спирта, эфира, серной кислоты, азотной кислоты, соляной кислоты, калийного щелока и пр., в стекле, меди, цинке и пр., Франкенгейм в большой работе 1835 г. попытался ввести новый специальный термин, синафия, для сцепления жидкостей и полагал, на основании своих опытов, что большему атомному весу соответствует меньшая синафия, а меньшей светопреломляющей способности — большая синафия. Позднее Деген доказал, что смачиваемость тела зависит от состояния его поверхности, сильно изменяясь от лежания на свободном воздухе, от трения различными телами, от полирования и т. д.
Такие же надежды и такие же трудности, как волосность, принесло открытие или, точнее, предпринятое вновь исследование эндосмотических явлений. Первое известие о подобном исследовании принадлежит Нолле, наблюдавшему в 1748 г. выравнивание воды и спирта через свиной пузырь. Г. Ф. Парро описал этот опыт и несколько других ему подобных в своем «Übersicht des Systems der theoretischen Physik» (Dorpat 1809—1811) («Обозрение системы теоретической физики»).
Фишер исследовал эти явления подробнее, но странным образом связал их с химическим действием. Если завязанную с одного конца пузырем стеклянную трубку наполнить водою и погрузить в сосуд с раствором медных квасцов, то, по Фишеру, происходит только постепенный переход медной соли в воду. Введение в трубку куска серебра не изменяет явления; но если серебро заменить металлом, который осаждает медь, например железом, то жидкость в трубке, бывшая в начале опыта на одном уровне с жидкостью сосуда, начинает постепенно прибывать и часа через два стоит уже на 2—3 дюйма выше. По мнению Фишера, это явление принадлежит к разряду тех, которые были открыты Эрманом и которые доказывают тождество основных причин механического сцепления и химического сродства. Несколько лет спустя Дютроше пришел на основании многочисленных опытов к заключению, что эти явления не могут быть связаны с изменениями уровней, так как через животный пузырь проходит не одна, а обе жидкости, но только с различными скоростями. Из физиков Дютроше первый определил совершенно правильно значение этих явлений, и он же дал им название эндосмоса и экзосмоса.
Из названных ученых каждый, за исключением Парро, делал открытие независимо от других; тем не менее, первенство долгое время приписывали именно Парро. На позднейшие нападки по этому поводу он ответил заявлением, что он никогда и не думал присваивать себе первенство открытия и что при появлении работы Дютроше он сам обратил внимание Парижской академии на открытие Нолле. Относительно причины эндосмотических явлений мнения долгое время расходились. Берцелиус сделал из опытов Фишера тот вывод, что рассматриваемые движения зависят от электрохимической противоположности между жидкостью и твердым телом. Дютроше искал сначала причину в своеобразной жизненной силе органических тканей, но когда нашел, что эти явления повторяются и при перегородках из обожженной глины, то стал приписывать эти явления особому действию электричества. Магнус считал основной причиной их волосность, так же думал и Пуассон. Дютроше признавал участие этого фактора, но полагал, что явления эндосмоса не могут быть полностью объяснены действием одного этого фактора.
Над газами соответствующие явления впервые наблюдал Грегэм (Graham) 6 в 1830 г. Закрыв один конец открытой трубки пробкой из гипса, высушенной при 93°, он наполнял ее исследуемым газом, опрокидывал в ртуть и наблюдал время, какое требовалось для обмена газа с атмосферным воздухом, а также отношение между замещающими друг друга объемами газов. При этом он установил следующий замечательный закон: взаимно обменивающиеся объемы газа и атмосферного воздуха обратно пропорциональны корням квадратным из плотностей обоих газов (отнесенных к атмосферному воздуху). Подобно гипсовым пробкам действовали и органические перепонки, но только при них диффузия происходила медленнее. В приложенной Грегэмом таблице плотности и обменивающиеся объемы приведены с точностью до 0,0001.
Берцелиус (Jahresbericht, XIV, стр. 84, 1834) заметил по этому поводу, что когда опыты заключают в себе так много источников ошибок, не стоит приводить тысячных долей. Позднее Бунзен тоже показал, что закон Грегэма действительно не вполне точен, так как в этих явлениях большую роль играет не только природа перегородок, но и величины давления обоих газов. Однако на основании механической теории газов этот закон должен быть верен, по крайней мере, для случая свободной дальтоновской диффузии, когда молекулярные силы перегородки не влияют на явление.
Действие молекулярных сил проявилось также в поглощении газов твердыми телами. Фузиньери и Беллани, констатировав большую трудность изготовления барометра, совершенно свободного от воздуха, сделали отсюда вывод, что воздух прилипает к поверхности твердых тел и остается на ней в виде неподвижного слоя. Фарадей объяснил так называемое каталитическое действие платины на гремучий газ существованием сгущенного слоя воздуха на поверхности частей платины. У. Генри пояснил это явление, указав, что неблагородные металлы не производят каталитического действия, так как они связывают химически притянутый их поверхностью кислород. Но тогда можно было ожидать, что, быть может, и при чисто механическом сгущении газов (давлением) молекулярные силы в газовых смесях будут доведены до того, что станут действовать наподобие химических. Однако Ленц и Парро, производившие в этом направлении опыты над смесями водорода и кислорода, пришли к определенно отрицательным результатам. Отсюда был сделан вывод о ничтожности находящихся в нашем распоряжении механических сил, по сравнению с величиной молекулярных сил. Такому представлению соответствовали и данные измерения сжимаемости жидких тел. После многих тщетных попыток Эрстеду5, наконец, удалось в 1822 г. получить более правильные данные о сжимаемости и упругости воды и других жидкостей. Этого он достиг тем, что производил давление не только на внутренность сосуда, но и на внешнюю поверхность последнего, чем было устранено растяжение сосуда. Как и предполагали, для сжимаемости воды по отношению к примененному давлению получилось очень маленькое число, именно при увеличении давления на 1 ат Эрстед получил уменьшение объема воды на 0,000047 первоначального объема. Несколько большее число было получено спустя несколько лет Колладоном и Штурмом, а именно 0,0000513.
В это же время стали изучать явления движения жидкостей под влиянием молекулярных сил. Савар первый наблюдал своеобразные явления на струях вытекающей воды. Описывая свое открытие, он говорит, что водяной луч, вытекающий из круглого отверстия в тонкой стенке, остается светлым только у самого выхода, а затем суживается, становится мутным и состоит из ряда продольных утолщений, поперечник которых больше диаметра выходного отверстия. Утолщения в непрозрачной части луча образуются из отдельных капель, которые принимают такую форму. Они образуются вследствие периодического ряда пульсаций, следующих друг за другом столь быстро, что они воспринимаются ухом как музыкальные тоны: скорость пульсации находится в прямом отношении к скорости вытекания и в обратном к диаметру отверстия. Когда два сосуда свободно опорожняются под равным давлением и водяные струи их направлены прямо навстречу друг другу, то истечение из обоих сосудов происходит одинаково, будут ли отверстия равны между собою или же нет, и имеют ли сосуды одинаковую или различную вместительность. Когда уровни воды в обоих сосудах поддерживаются на одной и той же высоте, то на месте встречи обоих лучей образуется плоский водяной слой; при разных же высотах, этот слой становится коноидальным или эллипсоидальным.
Наблюдая протекание газов по длинным трубкам, Баадер с удивлением заметил в 1805 г., что сопротивление, оказываемое трубками, сравнительно велико. Д'Обюиссон в результате тщательных опытов нашел, что это сопротивление пропорционально квадрату скорости газа и почти пропорционально длине трубки (оно возрастает несколько медленнее последней). Присасывание пластинок током воздуха, направленным на них из трубки, было, говорят, впервые замечено рабочим на литейном заводе Фуршамби (во Франции); Клеман сообщил об этом явлении и правильно его истолковал.
Эти, а равно и многие другие им подобные, а также более специальные опыты убедили ученых в значительной распространенности действия так называемых молекулярных сил, показав, что во всех физических явлениях, где замешаны действия на близком расстоянии, необходимо считаться с возможным влиянием подобных сил и принимать его в расчет. Экспериментальной физике даже удавалось во многих случаях изолировать действия этих молекулярных сил и очень правдоподобно объяснить ими явления. Но до ясного представления об этих силах, об их связи с понятием о материи и других элементарных силах ее тогда не дошли. Наоборот, чем больше стремились к созданию физики молекул, чем внимательнее изучали действия так называемых молекулярных сил, тем больше и больше трудностей возникало на пути к молекулярной физике.