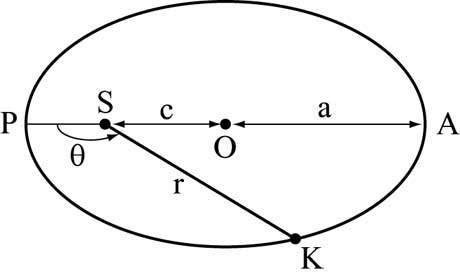
Первый закон. Планеты движутся по эллипсам, в общем фокусе которых находится Солнце.
Уравнение эллипса в полярной системе координат с полюсом в Солнце и с полярной осью, проходящей через перигелий, имеет вид:
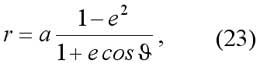
где e=c/a - эксцентриситет. Отсюда следуют выражения для минимального и максимального расстояния планеты от Солнца: q=a(1-e) и Q=a(1+e). Например, для орбиты Земли a=149,6x106 км, e=1/60, q=147,1x106 км и Q=152,1x106 км.
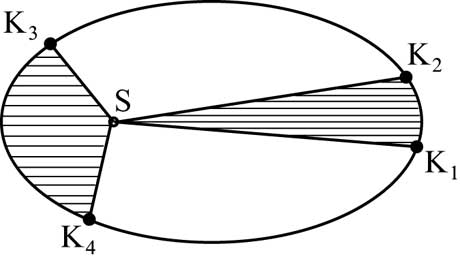
Второй закон (закон площадей): за одинаковые промежутки времени радиус-вектор планеты ометает равные площади. На рис.63 точки К1, К2, К3 и К4 - положения планеты в моменты t1, t2, t3 и t4 соответственно. Если t2-t1=t4-t3, то площади секторов К1SК2 и К3SК4 одинаковы. Из рис.63 видно, что дуга орбиты К3К4 длиннее дуги К1К2. Следовательно, чем ближе планета к Солнцу, тем больше ее скорость.
Второй закон можно записать в виде:
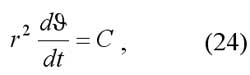
где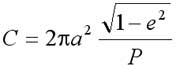 
и угол q выражен в радианах; Р - период обращения планеты вокруг Солнца.
Из второго закона Кеплера следует, например, что в перигелии скорость Земли в 1,0339 раз больше, чем в афелии (разность скоростей составляет примерно 1 км/с).
Третий закон: квадраты периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их орбит. Его можно записать так:
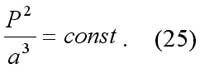
Если время выражать в периодах обращения Земли вокруг Солнца, а расстояния - в астрономических, единицах (1 а.е.= 149,6x106), то третий закон примет особенно простой вид: P=a3/2
Ньютон обобщил (и уточнил) все эти законы на случай двух произвольных материальных точек с массами m1 и m2, притягивающихся друг к другу по закону всемирного тяготения (других сил нет). Точки находятся по разные стороны от центра масс их системы, который делит отрезок, соединяющий точки, на части, длины которых обратно пропорциональны массам соответствующих точек. При этом каждая из них движется по эллипсу, в фокусе которого находится указанный центр масс, рис,64.
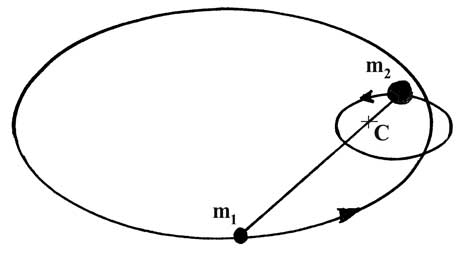
Однако при достаточно больших скоростях точек орбитами могут быть также парабола или гипербола.
Случаи, рассмотренные Кеплером соответствуют ситуации, когда начало системы отсчёта помещено в Солнце (например, в массу m1 рис.64). Планета же (масса её - m2) движется по эллипсу с фокусом в первой точке. Притяжения других планет не учитываются. Математическая запись уточнённого третьего закона Кеплера такова:
В таком виде закон применяют при определении масс двойных звёзд, а также масс планет, у которых имеется спутник. Пусть, например, P и a - период обращения и большая полуось относительной орбиты спутника данной планеты (или звезды). Тогда сумма масс планеты и спутника (или первой и второй звезды) может быть найдена по формуле:
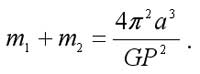
Как правило, массой спутника планеты можно пренебречь. Чтобы определить отношение масс звёзд, необходимо исследовать их орбиты относительно центра масс системы этих звёзд. Если a1 и a2 - большие полуоси соответствующих орбит, то справедливы равенства:
