1.2. Понятие первообразной функции и неопределённого интеграла
1.3. Интегралы, выражаемые и невыражаемые в элементарных функциях
1.4. Основные свойства неопределённого интеграла
2.1. Интегрирование путём сведения к табличным интегралам с помощью простейших преобразований
3.8. Метод алгебраических преобразований
4.1. Интегрирование линейных и дробно-линейных иррациональностей
4.1.1. Интегралы вида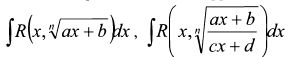 
4.1.2. Интегралы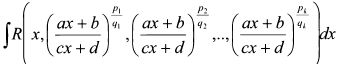 
4.2. Интегрирование квадратичных иррациональностей 
4.2.1. Интегралы вида 
4.2.2. Интегралы вида 
4.2.3. Интегралы вида 
4.2.4. Интегралы вида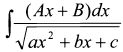 
4.2.5. Интегралы вида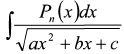 
4.2.6. Интегралы вида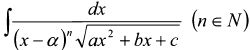 
4.2.7. Интегралы вида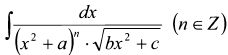 
4.2.8. Интегралы вида 
4.2.9. Интегралы вида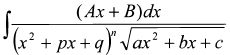 
4.2.10. Интегралы вида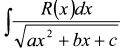 
4.2.11. Интегралы вида 
, а также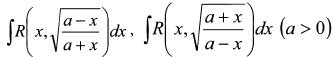 
4.2.12. Интегралы вида 
4.2.13. Интегралы вида 
, а также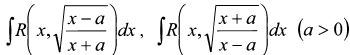 
4.2.14. 1-я подстановка Эйлера 
4.2.15. 2-я подстановка Эйлера 
4.2.16. 3-я подстановка Эйлера 
4.3. Интегрирование биномиальных дифференциалов 
4.4. Умножение на сопряжённое выражение, нестандартные подстановки и другие преобразования
5.1. Интегралы вида 
, где R - рациональная функция
5.1.1. Метод универсальной подстановки
5.1.2. Случай, когда 
5.1.3. Случай, когда 
5.1.4. Случай, когда 
5.2.1. Интегралы вида 
5.2.2. Случай, когда n и m - положительные чётные числа
5.2.3. Случай, когда n и m - натуральное нечётное число
5.2.4. Случай, когда n и m - целые отрицательные числа одной чётности
5.2.5. Интегралы вида 
5.2.6. Случай, когда n и m - целые отрицательные числа, причём одно из них нечётное
5.2.7. Случай, когда один из показателей - чётный, а другой - целый отрицательный
5.2.8. Случай, когда один из показателей - нечётный, а другой - целый отрицательный
5.5. Интегралы вида 
, где m - чётное натуральное число
5.11. Интегрирование по частям
6.1. Интегрирование гиперболических функций
6.2. Интегрирование показательных функций
6.3. Интегрирование логарифмических функций
6.4. Интегрирование обратных тригонометрических функций
Задачи для самостоятельного решения
, 
